Схема Бернулли

1. Понятие схемы Бернулли.

2. Теорема Бернулли.

3. Теоремы Муавра – Лапласа:

3.1. Локальная;

3.2. Интегральная.

4. Теорема Пуассона.

5. Алгоритм решения задач по схеме Бернулли.

1.

Задача: Укажите всевозможные исходы следующих испытаний:

А) игра в лотерею;

Б) один выстрел по мишени.

Решение. А) выигрыш, проигрыш;

Б) промах, попадание.

Пусть проводится любой эксперимент (σ), в котором только два исхода.

Согласно алгебре событий эти исходы будут противоположными событиями: А – успех, Ā – неуспех.

Обозначим Р(А) = р и Р(Ā) = q = (согласно свойствам вероятностей) = 1 – р

Наиболее известным примером испытаний Бернулли являются последовательные бросания правильной, т.е. симметричной монеты p = q = ½. В случае несимметричной монеты мы также считаем последовательные бросания независимыми, так что имеем испытания Бернулли, в которых вероятность успеха может быть произвольной.

Случайные извлечения с возвращением шаров из урны, содержащей r красных и k черных шаров, также являются испытаниями Бернулли с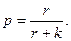

В случае бросания правильной игральной кости разбиение возможностей на выпадение 1 и невыпадение 1 приводит к испытаниям Бернулли с р = 1/6. Если кость несимметрична, то последовательные бросания также представляют собой испытания Бернулли, вероятности р и q изменят свои значения.