Изготовление шайб при серийном производстве также представляет бабой испытания Бернулли: успех - шайба годная, неуспех - шайба бракованная

Если рассматриваемый эксперимент удовлетворяет тому, что:

- проводимые испытания независимы;

- каждое испытание имеет два исхода;

- вероятность появления события в каждом испытании равна,

то говорят, что проводимый эксперимент удовлетворяет схеме независимых испытаний Бернулли.

2.

Задача: Вероятность выигрыша по одному билету денежно-вещевой лотереи равна р. Какова вероятность того, что из 4 приобретенных билетов два билета окажутся выигрышными?

Решение. Найдем вероятность согласно алгоритму решения задач на нахождение вероятностей сложных событий:

σ – игра в лотерею. Опыт проводится 4 раза.

А1 – выигрыш по первому билету;

А2 – выигрыш по второму билету;

А3 – выигрыш по третьему билету;

А4 – выигрыш по четвертому билету.

И соответственно:

Ā1 – проигрыш по первому билету;

Ā 2 – проигрыш по второму билету;

Ā 3 – проигрыш по третьему билету;

Ā 4 – проигрыш по четвертому билету.

Нужно найти вероятность того, что из четырех приобретенных билетов два билета окажутся выигрышными, т.е. Ā1 Ā2 А3 А4 + Ā1 А2 Ā 3 А4 + Ā1 А2 А3 Ā4 + А1 Ā2 Ā 3 А4 + А1 Ā2 А3 Ā4 + А1 А2 Ā3 Ā4.

Т.о., Р (Ā1 Ā2 А3 А4 + Ā1 А2 Ā 3 А4 + Ā1 А2 А3 Ā4 + А1 Ā2 Ā 3 А4 + А1 Ā2 А3 Ā4 + А1 А2 Ā3 Ā4)

Так как необходимо найти вероятность суммы событий, определяем совместность событий. События несовместны (в одном испытании не может произойти выигрыш и проигрыш по одному билету). Тогда

Р (Ā1 Ā2 А3 А4 + Ā1 А2 Ā 3 А4 + Ā1 А2 А3 Ā4 + А1 Ā2 Ā 3 А4 + А1 Ā2 А3 Ā4 + А1 А2 Ā3 Ā4) = Р (Ā1 Ā2 А3 А4)+Р(Ā1 А2 Ā 3 А4) + Р(Ā1 А2 А3 Ā4) + Р(А1 Ā2 Ā 3 А4)+

Р(А1 Ā2 А3 Ā4) + Р(А1 А2 Ā3 Ā4)

Так как необходимо также найти вероятность произведения событий, определяем зависимость событий. Поскольку события независимы (выигрыш (проигрыш) по одному билету не зависит от другого билета), то

Р (Ā1 Ā2 А3 А4 + Ā1 А2 Ā 3 А4 + Ā1 А2 А3 Ā4 + А1 Ā2 Ā 3 А4 + А1 Ā2 А3 Ā4 + А1 А2 Ā3 Ā4) = Р (Ā1 Ā2 А3 А4)+Р(Ā1 А2 Ā 3 А4) + Р(Ā1 А2 А3 Ā4) + Р(А1 Ā2 Ā 3 А4)+

Р(А1 Ā2 А3 Ā4) + Р(А1 А2 Ā3 Ā4) = Р (Ā1) Р(Ā2) Р(А3) Р(А4)+Р(Ā1) Р(А2) Р(Ā 3) Р(А4) + Р(Ā1) Р(А2) Р(А3) Р(Ā4) + Р(А1) Р(Ā2) Р(Ā 3) Р(А4)+Р(А1) Р(Ā2) Р(А3) Р(Ā4) + Р(А1) Р(А2) Р(Ā3) Р(Ā4) = qqpp + qpqp + qppq + pqqp + pqpq + ppqq = 6p²q²

Анализируя решенную задачу, можно получить для n независимых испытаний σ. Пусть k – число успехов, тогда n – k – число неуспехов. Отсюда

Рn (k) = Pn(k, n-k) *p *q = Cn *p *q - формула Бернулли.

Итак, полученная формула применяется, если рассматриваемый эксперимент удовлетворяет схеме Бернулли.

Задача: Вероятность выигрыша по одному билету денежно-вещевой лотереи равна 0.2. Какова вероятность того, что из 4 приобретенных билетов два билета окажутся выигрышными?

Решение. σ – игра в лотерею.

Опыт проводится n = 4 раза.

Проводимые испытания независимы (выигрыш (проигрыш) по одному билету не зависит от другого билета). В одном испытании может быть только два исхода – проигрыш, выигрыш. По условию задачи известно, что вероятность выигрыша по одному билету равна 0.2 и она постоянна. Таким образом условие данной задачи удовлетворяет схеме Бернулли.

Число успехов k = 2.

Тогда, Р4 (2) = C4 ² * p² * q² = 4!/2!*2!*0.2² *0.8² = 0.1536

Рассмотрим случай, что при проведении n независимых испытаний σ, удовлетворяющих схеме Бернулли, наступит не менее k1 и не более k2 раз.

Тогда Рn (k1 ≤ k ≤ k2) = ∑ Рn (k) =∑ Cn *p *q

Задача: Найдите вероятность осуществления от двух до четырех разговоров по телефону при наблюдении пяти независимых вызовов, если вероятность того, что разговор состоится, равна 0.7.

Решение. σ – разговоры по телефону.

Опыт проводится n = 5 раз.

Проводимые испытания независимы (разговор состоится (не состоится) не зависит от следующего разговора). В одном испытании может быть только два исхода – разговор либо состоится, либо не состоится. По условию задачи известно, что вероятность того, что разговор состоится равна 0.7 и она постоянна. Таким образом, условие данной задачи удовлетворяет схеме Бернулли.

Число успехов k1 = 2, k2 = 4.

Тогда Р5 (2 ≤ k ≤4) = Р5 (2) + Р5 (3) + Р5 (4) = C5 ² * p² * q³ + C5³ * p³ * q² +

C5 * p * q = 5!/2!*3!*0.7² *0.3² + 5!/3!*2!*0.7³ *0.3² + 5!/4!*1!*0.7 *0.3 ≈ 0.801

Пусть n – фиксированное, k может меняться {0, 1, 2,…n}.

Таким образом Рn(k) – функция от k. Тогда Рn(0), Рn(1), …, Рn(n) – можно говорить о наибольшем значении функции.

Отсюда, наивероятнейшем число успехов при данном числе опыте - µ.

np – q ≤ µ ≤ np + p

Задача: Магазин получил 50 деталей. Вероятность наличия нестандартной детали в партии равна 0.05. Найдите наиболее вероятное число нестандартных деталей в этой партии.

Решение. σ – определение на нестандартность деталей.

Опыт проводится n = 50 раз.

Проводимые испытания независимы (деталь нестандартная (стандартная) не зависит от следующей детали). В одном испытании может быть только два исхода – деталь либо стандартная, либо нестандартная. По условию задачи известно, что вероятность того, что в партии есть нестандартная деталь равна 0.05 и она постоянна. Таким образом, условие данной задачи удовлетворяет схеме Бернулли.

Так как нужно найти, наивероятнейшем число успехов при данном числе опыте - µ, то

np – q ≤ µ ≤ np + p

50*0.05 – 0.95 ≤ µ ≤ 50*0.05 + 0.05

1.55 ≤ µ ≤ 2.55

Так как число деталей может быть только целым, то наиболее вероятное число нестандартных деталей в этой партии равно 2.

3.1.

Задача: На некотором предприятии вероятность брака равна 0,05. Обследуется 500 изделий готовой продукции. Найти вероятность того, что среди них окажется ровно 25 бракованных.

Решение. σ – определение на брак изделий.

Опыт проводится n = 500 раз.

Проводимые испытания независимы (брак изделия не зависит от брака следующей детали). В одном испытании может быть только два исхода – деталь либо бракованная, либо нет. По условию задачи известно, что вероятность того, что на некотором предприятии вероятность брака равна 0,05 и она постоянна. Таким образом, условие данной задачи удовлетворяет схеме Бернулли.

По формуле Бернулли,

P_{500, 25} =C²⁵₅₀₀ (0, 05)²⁵(0, 95)⁴⁷⁵

Непосредственный подсчёт этого выражения представляет значительную техническую сложность, главным образом из-за громоздкости выражения для C²⁵₅₀₀ :

_500!

C²⁵₅₀₀ = ────.

^{25! 475!}

Полученное выражение для p _n,k имеет достаточно большую форму и может быть вычислено практически с помощью логарифмических таблиц.

Локальная приближенная формула Лапласа. При больших n имеет место приближенное равенство

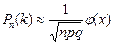, где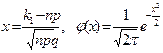

Замечание 1. На практике приближением Муавра-Лапласа пользуются при np > 10. Точность формулы растет, как с ростом величин n и k, так и по мере приближения величин p и q к 0.5.

Замечание 2. При нахождении значений функции j (х) для отрицательных значений аргументов следует иметь ввиду, что j(х) четная.

Возвратимся к рассмотренному ранее примеру, в котором фигурировала партия из 500 изделий; решение его было начато нами, но не доведено до конца. Ответ может быть получен теперь без особого труда. Учитывая, что в данном случае

25 - 25

np = 500 ∙ 0,05 = 25, npq = 25 ∙ 0,95 ≈ 24, x = ──── = 0,

√npq

получаем: 1

p₅₀₀(25) ≈ ─── φ (0) ≈ 0,08

√24

3.2.

Интегральная приближенная формула Лапласа. При больших n имеет место приближенное равенство P_n(k₁ k k₂)»Ф(х₂)–Ф(х₁), где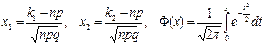

Функция Ф (х) называется функцией Лапласа.

Замечание 1. При нахождении значений функции Ф (х) для отрицательных значений аргументов следует иметь ввиду, Ф(x) - нечетная.

Замечание 2. Точность этой приближенной формулы растет с ростом n.

Замечание 3. Если np сравнительно невелико, то лучшее приближение дает формула

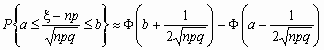и для вычисления вероятности того, что число успехов в n испытаниях Бернулли заключено между k ₁ и k ₂, можно использовать формулу

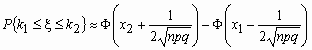, где , .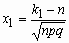

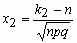◄Задача. Вероятность наступления события А в каждом из 900 независимых испытаний равна р == 0,8. Найдите вероятность того, что событие А произойдет: от 710 до 740 раз.