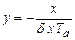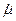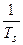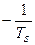Фазовое пространство и фазовая плоскость

Этот метод применим для систем с уравнениями не более второго порядка.

Переходные процессы, вызванные какими-либо начальными отклонениями координат (при отсутствии внешних воздействий), описываются нелинейными дифференциальными уравнениями динамики в нормальной форме

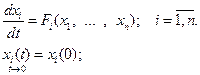(1.2.1)

где x_i – координаты состояния системы, 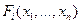- нелинейные функции.

Если координаты состояния x_i принять за координаты n-мерного пространства, то любой комбинации переменных 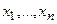соответствует определенное состояние или фаза системы, поэтому пространство называют фазовым.

		x 3,…, x n
		x 2
		x 1		Рис. 1.2.1

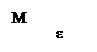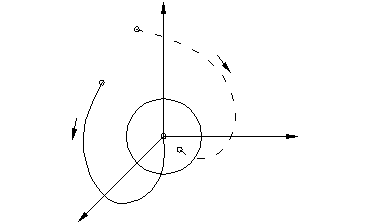
Точку М вn-мерном пространстве, характеризующую действительное (настоящее) состояние системы, называют изображающей. Изменению состояния системы соответствует движение точки 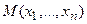по траектории, называемой фазовой. Совокупность фазовых траекторий называют фазовым портретом системы.

Для асимптотически устойчивых систем точка М движется по фазовым траекториям к началу координат.

В случае устойчивых систем точка М движется в область e вокруг начала координат.

По фазовым портретам системы можно судить об устойчивости движения.

Поскольку изображение n-мерного пространства практически невозможно, то наиболее широко распространен метод фазовой плоскости (n=2). Уравнения (1.2.1) при этом имеют вид:

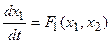; (1.2.2)

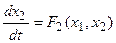; (1.2.3)

Дифференциальное уравнение фазовых траекторий получим, исключая время из уравнений (1.2.2 и 1.2.3), путём деления уравнения (1.2.3) на уравнение (1.2.2)

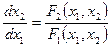; (1.2.4)

Большую информативность фазовых портретов даёт применение в качестве координат переменных 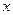и скорости её изменения 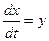, причём переменная у откладывается по оси ординат.

Система уравнений (1.2.4) при этом преобразуется к виду:

Рис. 2

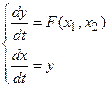(1.2.5)

Фазовая плоскость с этой системой координат обладает следующими свойствами:

а) в верхней полуплоскости (рис.1.2.2) направление движения по траекториям слева направо, т.е. в сторону увеличения x, так как там скорость y >0, а в нижней полуплоскости, наоборот, – справа налево

б) ось x пересекается фазовыми траекториями под прямым углом, т.к. в точках пересечения скорость y =0, т.е. имеет место максимум или минимум величины x.

Рис.1.2.2

e

1.3. Типы особых точек и фазовые траектории линейных систем

Рассмотрим линейную систему, движение в которой описывается уравнением:

Решим уравнение (1.8) относительно старшей производной

Введем новую переменную

, =

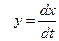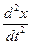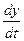
Разделим (1.10) на (1.11) и получим дифференциальное уравнение (ДУ) фазовых траекторий

Решение y = f(x) этого ДУ определяет собой некоторое семейство интегральных кривых на фазовой плоскости (x,y), каждая из которых соответствует одному определенному значению произвольной постоянной. Совокупность интегральных кривых (фазовый портрет) представляет собой все возможные фазовые траектории, а значит все возможные виды переходных процессов в замкнутой САУ при различных начальных условиях..

В точках, соответствующих установившемуся состоянию (x=0, y=0), получаем согласно уравнению (1.12) выражение

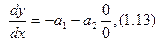
то есть неопределенное направление касательных к интегральным кривым. Эти точки называют особыми и они классифицируются, т.е. им присвоены названия.

Уравнению (1.8) соответствуют корни характеристического уравнения

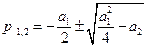(1.14)

В зависимости от знаков и величины коэффициентов a₁ и а₂ возможны шесть случаев корней характеристического уравнения и соответствующих им фазовых траекторий.

Рассмотрим эти случаи подробнее:

1) a₁=0, a₂>0 – корни чисто мнимые.

Линейная система на границе устойчивости (в системе возникают незатухающие колебания).

2) a₁>0, a₂>0, дискриминант D <0 – корни комплексные с отрицательными вещественными частями. Линейная система устойчива, процессы колебательные, затухающие.

3) a₁<0, a₂>0, дискриминант D <0 – корни комплексные с положительными вещественными частями.

Линейная система неустойчива, процессы колебательные расходящиеся.

4) a₁>0, a₂>0, дискриминант D >0 – корни вещественные, отрицательные.
Линейная система устойчива, процессы апериодические.

5) a₁<0, a₂>0, дискриминант D >0 – корни вещественные, положительные.
Линейная система неустойчива, процессы апериодические.

6) a₁>0, a₂<0, D >0 – корни вещественные, разных знаков. Линейная система неустойчива, процессы апериодические.

Рассмотрим фазовые траектории для каждого случая в отдельности.

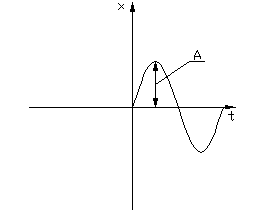1. Если рассматривать движение от оси абсцисс, то можно записать 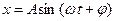, , 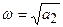а величины А и 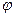определяются начальными условиями.

Рис. 1.3.1.б

Рис. 1.3.1а

wA

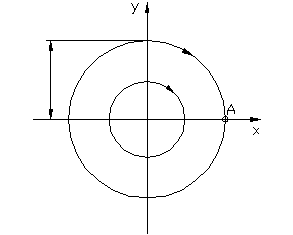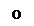
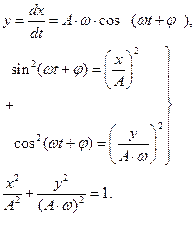
Незатухающим колебаниям в системе (рис.1.3.1а) соответствует движение изображающей точки М (рис.1.3.1б) по замкнутым траекториям эллиптического вида.

Точка О (x=0; y=0) – особая точка, центр.

2. Корни комплексные с отрицательными вещественными частями

		О
	Рис. 1.3.2 а
		Рис. 1.3.2 б

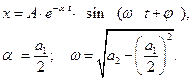
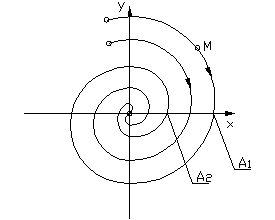
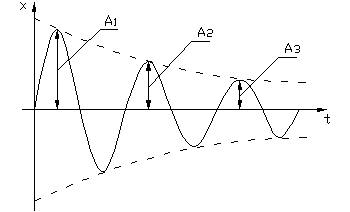
А₁> А₂>…> А_n

Затухающим колебаниям (рис.1.3.2а) в системе на фазовой плоскости (рис.1.3.2.б) соответствуют спиралевидные траектории, по которым изображающая точка стремится к началу координат. Точка О – особая точка – устойчивый фокус.

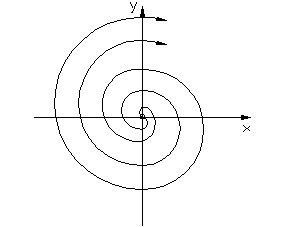
3. Корни комплексные с положительными вещественными частями.

	Рис. 1.3.3 а		Рис. 1.3.3 б

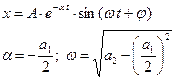
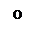Расходящимся колебаниям в системе на фазовой плоскости соответствуют спиралевидные траектории, по которым изображающая точка удаляется от начала координат. Особая точка О – неустойчивый фокус.

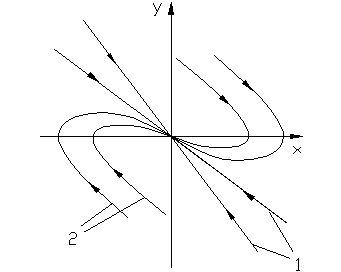
4. Корни вещественные, отрицательные.

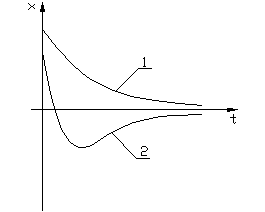
Переходные процессы апериодические двух типов: монотонные (1) и с перерегулированием (2).

y=a2x

Рис. 1.3.4 б

Рис. 1.3.4 а

y=a1x

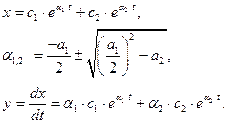
Монотонные процессы получаются при выполнении условий:

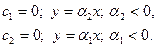
Соответствующие им фазовые траектории имеют вид прямых линий (рис.1.3.4б).

Особая точка О – устойчивый узел.

Фазовые траектории, имеющие точку равновесия в виде устойчивого узла, соответствуют апериодическому затухающему переходному процессу.

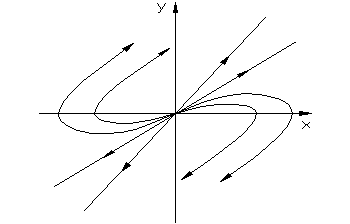
5. Корни вещественные, положительные.

Рис. 1.3.5 б

Рис. 1.3.5 а

y=a2x

y=a1x

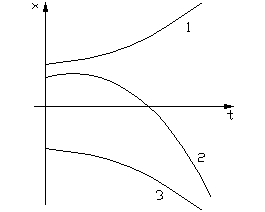
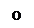
Выражения такие же, как в предыдущем случае, только α меняет знак

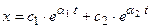
Движение изображающей точки направлено от точки равновесия системы к бесконечной удаленной точке фазовой плоскости. В этом случае положение равновесия системы неустойчивое.

Особая точка О – неустойчивый узел.

6. Корни вещественные разных знаков.

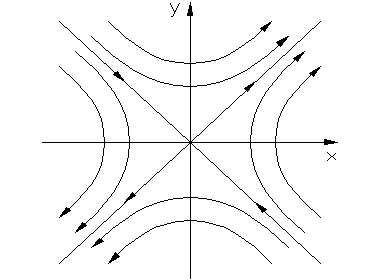Процессы апериодические неустойчивые (рис.1.3.6а).

Рис. 1.3.6 б

Рис. 1.3.6 а

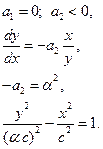
Где С- постоянная интегрирования.

Фазовые траектории имеют вид гипербол.

Рис. 10

Особая точка О называется «седло».

Седло всегда неустойчиво.

e

1.4. Особые линии в нелинейных системах

Во многих случаях реальные САУ можно считать линейными лишь при малых отклонениях перемененных от их заданных значений в установившемся состоянии. При этом их фазовые портреты соответствуют особым точкам линейных систем. При больших отклонениях из-за наличия нелинейностей характер движений и фазовые портреты могут существенно отличаться от портретов линейных систем, при этом возможны следующие случаи:

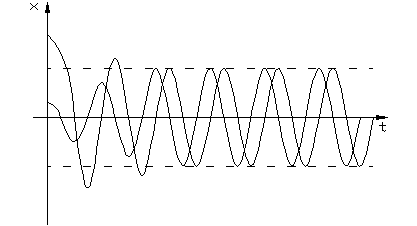
1. Устойчивый граничный периодический режим с амплитудой колебаний а₁.

а1

Рис. 1.4.1 а

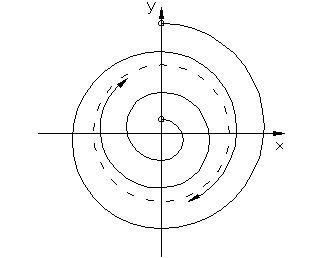При малых начальных отклонениях 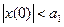система может оказаться неустойчивой. Поэтому согласно линейной теории колебания начинают расходиться, но из-за наличия нелинейности их амплитуда ограничивается предельной величиной а₁. При больших начальных отклонениях 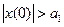система становится устойчивой и колебания затухают, но не до нуля, а до а ₁. Т.е. система генерирует колебания с постоянной амплитудой и частотой, которые называют автоколебаниями.

Картина фазовых траекторий, соответствующая такому случаю имеет вид (рис.1.4.1б).

а1

Вблизи начала координат имеют место спирали как в неустойчивой линейной системе с особой точкой «неустойчивый фокус». Но далее они расходятся не до бесконечности, а приближаются асимптотически к некоторому замкнутому контуру ограниченных размеров.

Рис. 1.4.1 б

К нему же приближаются спирали вне контура (устойчивый фокус). Т.е. на фазовом портрете нелинейной системы наблюдаются несколько особых точек линейных систем.

Устойчивым автоколебаниям на фазовой плоскости соответствует замкнутая траектория, к которой стремится изображающая точка, независимо от амплитуды начальных отклонений. Эта замкнутая траектория представляет первый тип особых линий и называется устойчивый предельный цикл. Размеры предельного цикла по осям координат представляют амплитуду колебаний а₁ и скорость её изменения. Для нахождения периода колебаний нужно решить дифференциальные уравнения системы.

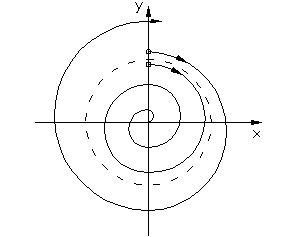
2. Неустойчивый граничный периодический режим с амплитудой а₂. Равновесное состояние (х=0) системы устойчиво в «малом», т.е. и неустойчиво в «большом», т.е. 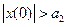. Здесь граничным процессом является неустойчивый периодический режим собственного движения системы с амплитудой а₂.

	Рис. 1.4.2 б

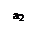Система устойчива в «малом» и неустойчива в «большом», неустойчивому периодическому режиму соответствует 2-ой тип особых линий – неустойчивый предельный цикл.

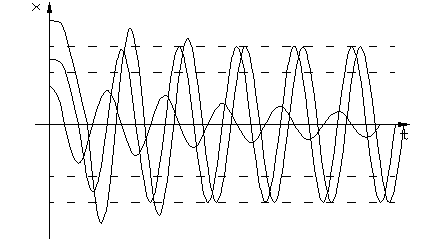
3. Если переходные процессы имеют вид (рис.1.4.3 а), то на фазовой плоскости им соответствуют два предельных цикла (ПЦ): неустойчивый ПЦ с амплитудой а₁ (рис.1.4.3б) и устойчивый ПЦ с амплитудой а₂.

	а2
	а1
		Рис. 1.4.3 а
		Рис. 1.4.3 б бю

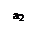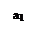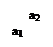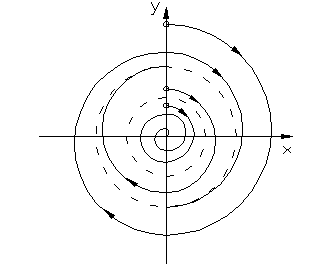В соответствии с рис.1.4.3 б система устойчива в «малом» и автоколебательна в «большом».

4. Апериодические процессы.

В случае апериодических процессов также возможны устойчивые и неустойчивые предельные циклы, при этом при различных амплитудах начальных отклонений процессы могут становиться либо колебательными, либо апериодическими.

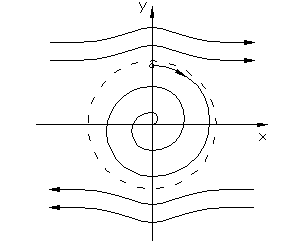
В нелинейной системе при больших отклонениях переменных колебательные процессы могут переходить в апериодические (рис. 1.4.4 а,). На фазовой плоскости наблюдается неустойчивый ПЦ (рис.1.4.4.б).

	а1
		а1

	Рис. 1.4.4 а
		Рис. 1.4.4 б

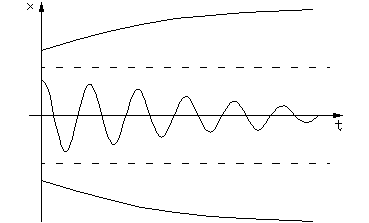
Система устойчивы в «малом» и неустойчива в «большом».

5. Система согласно линейной теории находится на границе устойчивости.

.

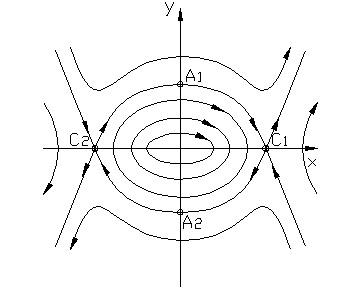
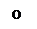Вблизи начала координат наблюдаем фазовые траектории типа «центр». При удалении от начала координат возникают два седла С ₁, С ₂, что приводит к фактической неустойчивости системы. Но может иметь место и устойчивый предельный цикл А₁С₁А₂С₂, который образован двумя сепаратрисами С₂А₁С₁ и С₁А₂С₂.

Лини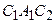и и 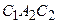, разделяющие фазовые траектории разных типов называют сепаратрисами – третий вид особых линий.

Рис. 1.4.5

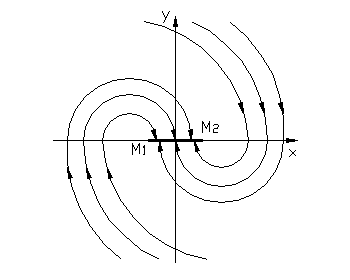
6. Для ряда нелинейных систем с зонами нечувствительности (рис.1.4.6.а), люфтом, сухим трением характерно отличие от рассмотренных случаев, состоящее в том, что в них приближение к линейной системе наступает, при достаточно больших отклонениях переменных, т.е. их можно рассматривать как линейные в «большом», а не в «малом».

	Рис. 1.4.6 а
		Рис. 1.4.6 б

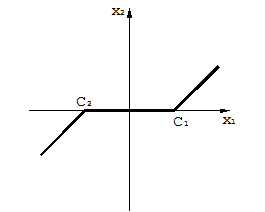
Наличие зоны нечувствительности проявляется в том, что установившемуся состоянию равновесия при данной нагрузке соответствует не одна точка на фазовой плоскости (рис.1.4.6.б), а отрезок состояний равновесия, т.е. изображающая точка попадает не в начало координат, а на отрезок покоя М₁М₂, при этом система не обладает асимптотической устойчивостью. Длина этого участка зависит от ширины зоны нечувствительности.

Глава 2. Фазовая плоскость систем, описываемых уравнениями с неаналитической правой частью

В дифференциальных уравнениях с неаналитической правой частью, последняя не раскладывается в ряды по степеням аргументов (х,у).

e

2.1. Исследование системы со скользящим режимом

Рассмотрим систему, которая содержит объект с самовыравниванием, безынерционный чувствительный элемент, усилитель мощности (золотник) и серводвигатель постоянной скорости.

j - регулируемая переменная

h - выходная величина чувствительного элемента

s - выходная величина У.М.

m - регулирующее воздействие

В общем случае объект управления с самовыравниванием описывается уравнением: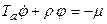

Где:

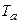- постоянная времени,

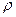- коэффициент самовыравнивания,

- если r>0 – объект статически устойчив, и задачей регулятора является обеспечение требуемого качества управления;

-если r<0 – объект статически неустойчив,

-если r=0 – объект нейтрален.

В двух последних случаях задачами регулятора являются: во-первых, обеспечение устойчивости, во-вторых, обеспечение требуемого качества управления.

Рассмотрим случай нейтрального объекта т.е. r=0, тогда:

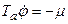. (2.1.1)

Уравнение серводвигателя постоянной скорости 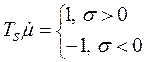(2.1.2)

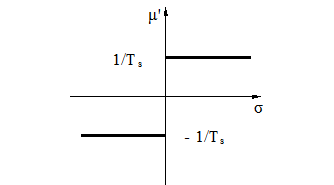
Уравнение золотника с жесткой обратной связью 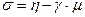(2.1.3)

γ – коэффициент жесткой обратной связи

Уравнение безынерционного чувствительного элемента (ЧЭ)

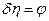(2.1.4)

d - коэффициент, характеризующий чувствительность ЧЭ

Исключим промежуточные переменные μ, σ, η

Для этого, продифференцировав уравнение (2.1.1), решим (2.1.1, 2.1.2, 2.1.3, 2.1.4) относительно старшей производной выходной переменной и получим:

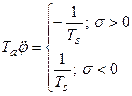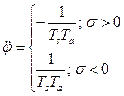; ; (2.1.5)

Исключим переменную σ:

Таким образом,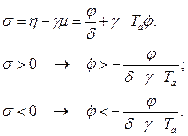

С учетом изложенного

(2.1.6)

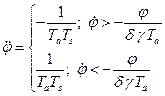Заменим переменные

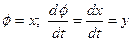
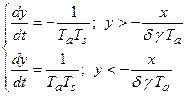(2.1.7)

Учитывая что 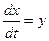, (2.1.8)

исключим в (2.17) переменную время t. Для этого разделим выражения (2.1.7) на (2.1.8):

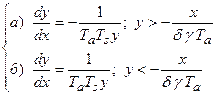(2.1.9)

Проинтегрируем выражения (2.1.9), получим уравнения интегральных кривых, определяющих траектории на фазовом портрете

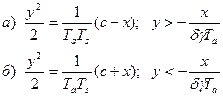(2.1.10)

Уравнение линии переключения получим, заменяя в условии 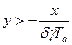знак неравенства знаком равенства:

Рис. 2.1.2

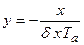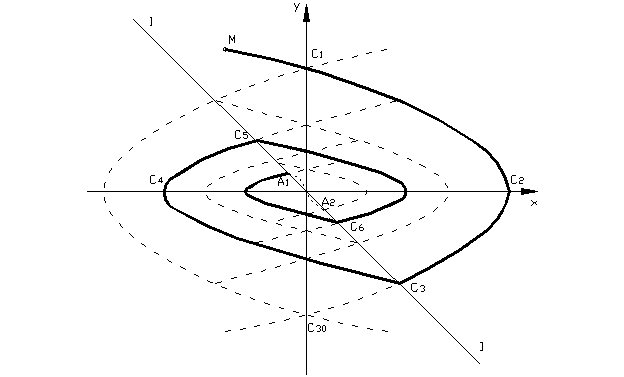
(2.1.11)

Рассмотрим фазовый портрет системы. Область справа от линии переключения I-I заполнена траекториями (параболами) семейства 2.1.10а, а слева – семейства 2.1.10б.

При отсутствии внутренней жесткой обратной связи линия переключения совпала бы с осью ординат и точка М, двигаясь по траектории С₁С₂С₃₀ семейства 2.1.10а, переходила бы в точке С₃₀, на симметричную траекторию С₃₀С₁ семейства 2.1.10б. Этой замкнутой траектории соответствовали бы автоколебания в системе. Из-за наличия внутренней обратной связи (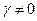), переход с параболы семейства 2.1.10а на параболу семейства 2.1.10б происходит на линии переключения в точке С₃ и, двигаясь по параболе С₃С₄С₅, а в точке С₅ происходит переход на траекторию семейства 2.1.10а и т.д. С каждым полуколебанием изображающая точка приближается к началу координат – к равновесному состоянию. Это соответствует о затухающим колебаниям в системе. Однако, при попадании точки М на отрезок А₁А₂, характер движения становится существенно иным.

Точки А₁ и А₂ являются точками пересечения линии переключения I-I с параболами семейства 2.1.10а и 2.1.10б, проходящими через начало координат.

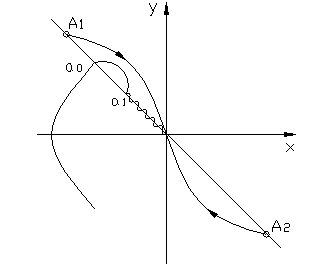Если изображающая точка М попадает на особый отрезок А₁А₂, например, в точку а₀, то в дальнейшем изображающая точка скользит вдоль линии переключения из-за непрерывного реверсирования серводвигателя.

Начиная с точки А₁, начинается скользящий режим. Скольжение происходит по линии переключения до начала координат.

Рис. 2.1.3

Найдем закон движения в скользящем процессе. На линии переключения уравнение движения будет иметь вид: 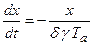. (2.1.12)

Рис. 20

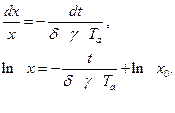
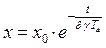,. (2.1.13)

– является решением уравнения (2.1.12).

Значения x ₀ и t отсчитываются с момента попадания точки М на линию скользящего режима.

Особенность скользящего режима заключается в том, что в данном режиме нелинейная колебательная система 2-го порядка вырождается в линейную систему первого порядка. При этом закон движения в скользящем режиме не зависит от параметров прямой цепи системы и определяется только коэффициентом обратной связи.

e

2.2. Исследование релейной системы

Рассмотрим фазовую плоскость системы, в которую входит объект управления с самовыравниванием, безынерционный чувствительный элемент, золотник с ЖОС и серводвигатель постоянной скорости с симметричной мертвой зоной.

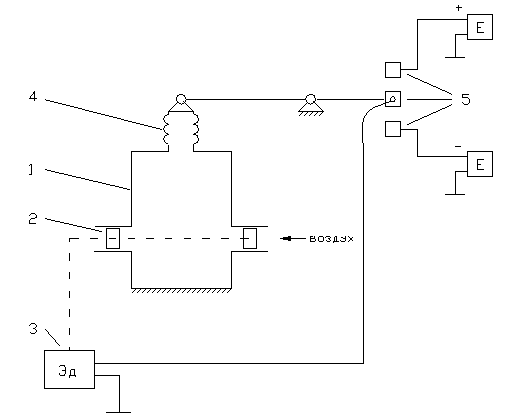
В качестве примера рассмотрим регулятор давления воздуха в баллоне.

	Рис. 2.2.1

1 – баллон, 2 – заслонки, 3 – электродвигатель, 4 – сильфонный манометр,

5 – релейно-контактное устройство

Количество поступающего в баллон 1 воздуха регулируется заслонками 2, которые приводятся в движение электродвигателем 3. Управление электродвигателем осуществляется релейно-контактным устройством 5, играющим роль золотника, а чувствительным элементом служит сильфонный манометр 4.

Уравнение объекта управления с самовыравниванием

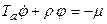(2.2.1)

Уравнение серводвигателя с симметричной мертвой зоной:

s0

-s0

s

(2.2.2)

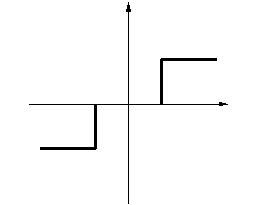
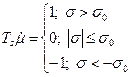	Рис. 2.2.2

Уравнение безынерционного чувствительного элемента:

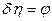(2.2.3)

Уравнение золотника с ЖООС:

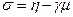(2.2.4)

Избавимся от промежуточных переменных μ, σ, η

Продифференцируем уравнение (2.2.1)

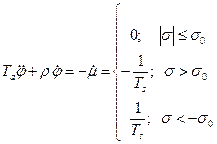
Избавимся от σ:

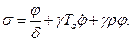Таким образом условия переключения имеют вид:

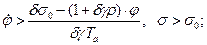
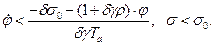
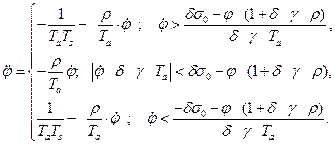(2.2.5)

Введем новые переменные: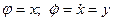

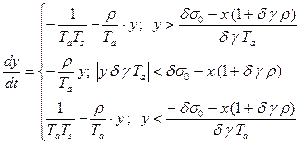(2.2.6)

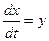. (2.2.7)

Исключим переменную t:

(2.2.8) (2.2.9) (2.2.10)

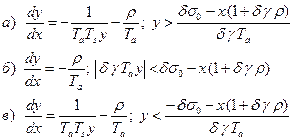
Рассмотрим на примере выражения (2.2.10) процедуру интегрирования

	(2.2.11) (2.2.12) (2.2.13)

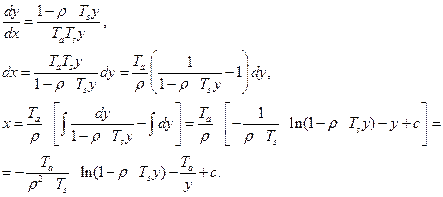
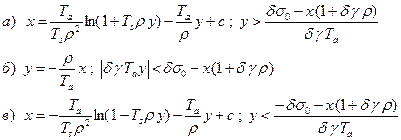
Заменим в условиях определения знаки неравенства равенствами

и получим две линии переключения:

(2.2.17) (2.2.18)

	Рис. 2.2.3

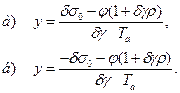
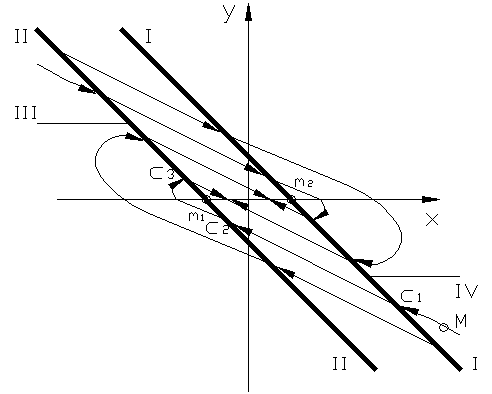I-I – линии переключения (2.2.17)

II-II – линии переключения (2.2.18)

Область справа от линии переключения I-I заполнена фазовыми траекториями семейства 2.2.11. Область слева от линии переключения II-II заполнена фазовыми траекториями семейства 2.2.13, а между линиями переключения – прямыми семейства 2.2.12.

Кроме двух линий переключения I-I и II-II появляются особые прямые III и IV в семействе (2.2.11) и (2.2.13), особенность их в том, что фазовые траектории, находящиеся в области над или под ними не могут перейти через них.

Рассмотрим движение точки М семейства (2.2.11), .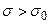

В точке С₁ серводвигатель выключается и движение в системе происходит за счет инерции объекта по траектории С₁С₂ семейства (2..212). В точке С₂ происходит обратное включение серводвигателя, он реверсируется и движение идет по траектории С₂С₃ семейства (2.2.13). В точке С₃ серводвигатель выключается, и изображающая точка по прямой (2.2.12) попадает на отрезок покоя m₁m₂, и движение заканчивается. Система устойчива, но наличие отрезка покоя, соответствующего состоянию равновесия, может привести к увеличению установившейся ошибки сверх требуемой величины.

e

2.3. Многолистное фазовое пространство

В рассмотренном ранее случае система описывалась дифференциальным уравнением, в котором правая часть является однозначной функцией своих аргументов. Однако, в нелинейностях типа люфт, зазор или сухое трение правая часть является неоднозначной функцией аргументов и не может быть отражена на обычной фазовой плоскости (на одном листе). В этих случаях используется многолистное фазовое пространство.

Рассмотрим систему, содержащую объект без самовыравнивания (2.3.1), серводвигатель постоянной скорости (2.3.2), золотник (2.3.4) и безынерционный чувствительный элемент(2.3.3).

Уравнение объекта

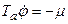. (2.3.1)

Уравнение серводвигателя

s

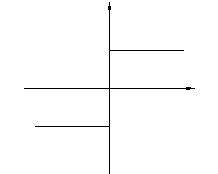
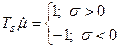(2.3.2)

Уравнение чувствительного

элемента

Рис. 2.3.2

Рис. 2.3.1

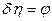. (2.3.3)

s

Уравнение золотника

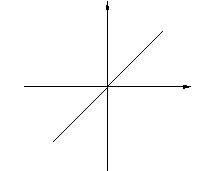
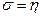(2.3.4),

представляет собой биссектрису

координатного угла.

	h

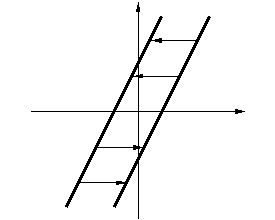
Предположим, что между ЧЭ и золотником имеется люфт. Величина люфта равна m, тогда график люфта (рис. 2.3.3) выглядит следующим образом:

s

a1

- 0.5 m

h

a2

0.5 m

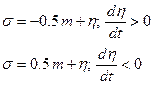(2.3.5)

	a3
		a4
		Рис. 2.3.3

Объединяя уравнения (2.3.1), (2.3.2), (2.3.3), (2.3.5), исключим промежуточные переменные m, s, h, тогда получим:

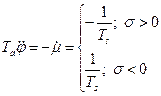
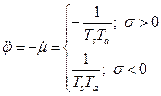(2.3.6)

Исключим переменную s.

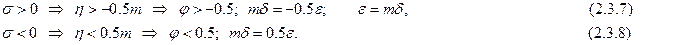
В результате получим систему уравнений:

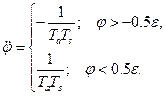(2.3.9)

Произведём замену переменных

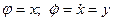
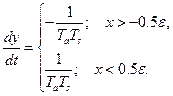(2.3.10)

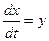(2.3.11)

Избавимся от времени t, разделим (2.3.10) на (2.3.11), получим дифференциальные уравнения фазовых траекторий:

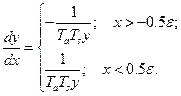(2.3.12)

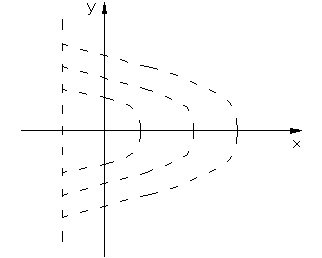
После интегрирования получим два семейства парабол

(2.3.13) (2.3.14)

	0.5 e -0.5 e

	Рис. 2.3.4

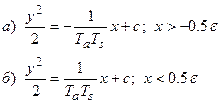
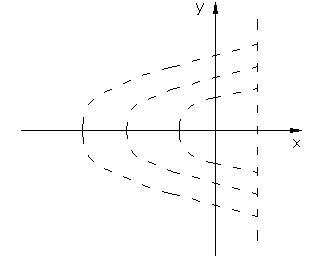
Как видно из рис. 2.3.4 фазовые траектории семейства 2.3.13 и 2.3.14 перекрывают друг друга в диапазоне 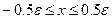, что создает неоднозначность в построении фазового портрета системы. Для устранения неоднозначности в этой полосе, фазовые траектории строят на разных листах, потом их накладываются один на другой так, чтобы совпали координатные оси.

		Рис. 2.3.5

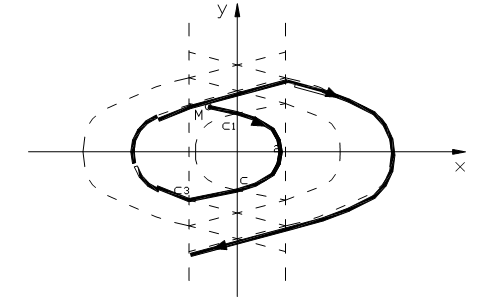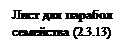Если бы не было люфта, то точка М, двигаясь по траектории С₁С₂ семейства (2.3.13), переходила бы на траекторию семейства (2.3.14) в точке С₂ и движение на фазовом портрете происходило бы по замкнутой траектории (устойчивый предельный цикл), а в системе бы возникали автоколебания. Из-за наличия люфта точка М переходит с одного листа на другой только на границах соответствующего листа x=0.5 e и x= -0.5 e. При этом получаемая расходящаяся траектория соответствует неустойчивым процессам в системе (расходящиеся колебания).

В итоге делаем вывод, что люфт – явление вредное и, обычно, приводит к автоколебаниям в системе.

e

Глава 3. Метод точечных преобразований

- метод связан с методом фазовых плоскостей.

Рис. 31б

Рис. 31а

Рис. 3.1

Пусть точка М в начальный момент времени находится в точке О₁ на линии переключения ОР. Через период колебаний точка М будет находиться в точке О₂. Так как через каждую точку фазового пространства можно провести только одну фазовую траекторию, то обходу точки М вокруг начала координат соответствует переход каждой точки полупрямой ОР в другую точку этой полупрямой. Такой переход называют точечным преобразованием полупрямой ОР в саму себя. Если при этом некоторая точка полупрямой преобразуется сама в себя, то этой неподвижной точке преобразования соответствуют автоколебания в системе (устойчивый предельный цикл).

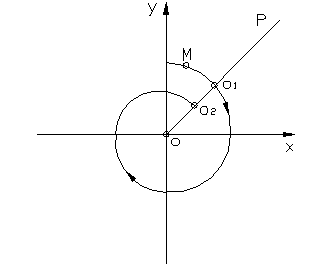
Исходной точке О₁ соответствует определенное расстояние от до начала координат. Если обозначить расстояние ОО₁=S, а расстояние от начала координат до последующий точки обозначить через S` (ОО<sub>2</sub>=S`), то точечному преобразованию полупрямой ОР можно поставить в соответствие на плоскости S`S некоторую кривую S`=f(S), называемую функцией последования.

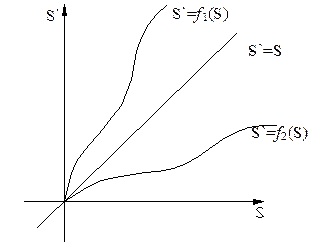
Неподвижным точкам точечного преобразования (предельного цикла) соответствует преобразование S`=S или биссектриса координатного угла.

Взаимное расположение функции последования и биссектрисы S`=S определяет характер движения в системе.

Рис. 3.2

Если функция последования f(S)= f₂(S) лежит ниже биссектрисы S`=S, то процессы затухающие, система устойчива.

Если f(S)=f₁(S) лежит выше биссектрисы S`=S, то процессы расходящиеся, система неустойчива (автоколебаний нет).

Если f(S) пересекает биссектрису S`=S, то возможны автоколебания.

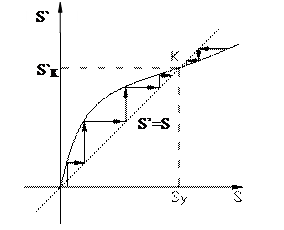
Для определения характера движения (устойчивости) можно построить лестницу Ламерея.

Для этого необходимо отложить на оси абсцисс значение S, затем провести вертикальную прямую до кривой последования и найти значение S’. Принять это значение S’ за новое S (провести горизонтальную линию до биссектрисы S’= S) и повторить построение, и по которой изображающая точка стремится к началу координат, или удаляется от него.

	Рис. 3.3 а

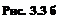
В точке К (рис.3.3а) выполняется условие 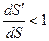- колебания устойчивы.

В точке N выполняется условие 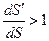, что соответствует неустойчивым автоколебаниям.

Функцию последования S`=f(S) в большинстве случаев легче представить в параметрической форме. При этом в качестве параметра используется время τ – время прохождения изображающей точкой по фазовой траектории расстояния от исходной точки О<sub>1</sub> до последующей точки О<sub>2</sub>. При этом S= f <sub>1</sub>(τ), S`= f ₂(τ). Для определения характера движения в этом случае также строится лестница Ламерея.

Если функции S`(τ) и S(τ) не пересекаются, то автоколебаний нет.

Если S(τ)> S`(τ), то колебания затухающие, система устойчива.

Если S(τ)< S`(τ), то колебания расходящиеся (рис.3.4), система неустойчива.

		Рис. 32
		Рис. 3.5а		Рис. 3.5б
	Рис. 33а
		Рис. 34

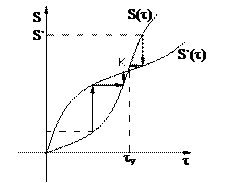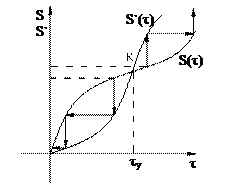
Если кривые S= f ₁(τ), S`= f ₂(τ) пересекаются, то возможны автоколебания. При выполнении условия 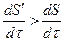- автоколебания неустойчивы (точка К, рис.3.5а). И автоколебании устойчивы при 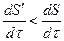(точка К, рис.3.5.б).

На рис.3.6 показан случай двух точек пересечения кривых S= f ₁(τ) и S`= f ₂(τ). При этом в точке K – неустойчивый предельный цикл, в точке N – устойчивый предельный цикл.

Система устойчива в «малом» и автоколебательна в «большом».

Функция последования находится путем интегрирования дифференциальных уравнений системы. Этот метод также как и метод фазовой плоскости используется для систем не выше второго порядка.

e

Глава 4. Автоколебания в системах высокого порядка