Метод бисекции (метод деления отрезка пополам)

Задача заключается в нахождении корней нелинейного уравнения

.

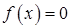Для начала итераций необходимо знать интервал 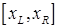значений , на концах которого функция принимает значения разных знаков:

(*)

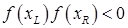Из непрерывности функции 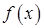и условия (*) следует, что на интервале 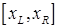существует хотя бы один корень уравнения. В случае монотонности функции на этом интервале корень будет единственным.

Выбреем точку внутри интервала

.

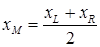Если 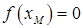, то корень найден. Если 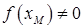, разобьем этот интервал на два 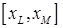и 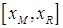. Теперь найдем новый интервал, в котором функция меняет знак. Пусть 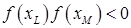и соответственно корень находится внутри интервала 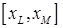. Тогда обозначим 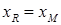и повторим описанную процедуру до достижения требуемой точности. За количество итераций 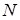первоначальный отрезок делится в 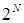раз.

Программный код

xl – начало отрезка по х;

xr – конец отрезка по х;

xm – середина отрезка по х;

eps,eps1 – требуемая точность вычислений.

Алгоритм можно записать следующим образом (в псевдокоде):

1.Начало.

2.Ввод хl, xr, eps.

3.Если |F(хl)| < eps, то Вывод (корень уравнения – xl).

4.Если |F(хr)| < eps, то Вывод (корень уравнения – xr).

5.Пока |F(хm)| > eps или |xr-xl| > eps1 повторять:

6.xm:= (xr+xl)/2;

7.если (F(xl)*F(xm) < 0), то xr:= xm;

8.если (F(xm)*F(xr) < 0), то xl:= xm.

9.Вывод (Найден корень уравнения – xm точности ε).

10.Конец.