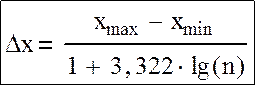Этапы моделирования непрерывных случайных величин

Сначала нужно установить величину элементарного интервала, то есть интервалы изменения x, соответствующего i ^ому событию. Всего таких интервалов должно быть k, значит, первый этап связан с организацией полной группы событий. Существует несколько эмпирических методик получения таких интервалов. Например, формула Стерджесса для нахождения оптимальной величины интервала:

где n – объем выборки, (x_max-x_min) образуют размах колебания изучаемого признака R. Отсюда:

Здесь k нельзя считать группой событий, так как это количество групп вариационного ряда. В этом ряду x_i располагаются по возрастанию. На практике часто необходимо округлить k, а значит изменить значение ∆x. Если необходимо, можно изменить левую и/или правую границы размаха колебаний. По другой методике количество интервалов должно быть в 5-10 раз меньше числа опытов. Далее нужно определить частоты, то есть количество наблюдений за попаданием случайной величины в i ^ый интервал.

Отношение частот к объему выборки называется относительной частотой:

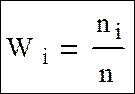
Тогда статистическим распределением выборки будет являться перечень-вариант из соответствующих ему частот, или относительных частот.

Графиком такого распределения является либо полигон частот, либо гистограмма. Полигон частот – это ломаная линия, отрезки которой соединяют точки (x_i, n_i).

Гистограмма частот – это ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат частичные интервалы длиною ∆x, а высоты равны плотности частоты n_i/∆x. Существует также плотность относительной частоты, то есть W_i/∆x. Проверкой правильности построения гистограммы является равенство площади гистограммы единице.

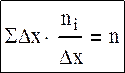
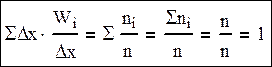
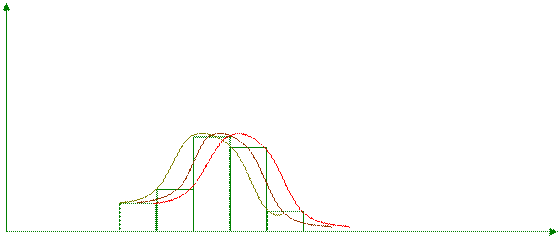
Пусть гистограмма имеет вид:

W_i

x

При построении теоретической кривой распределения предпочтение отдается центрам каждого единичного интервала. Если пограничные интервалы содержат малое число n_i, то такие интервалы следует укрупнить. При расчете n_i можно реализовать две методики:

· Отнесение пограничных значений x_j к левой границе соответствующего интервала (обычно выполняются по умолчанию).

· Позиционирование по правой границе интервалов (обычно специально оговаривается). Следует о том, что вероятностью при исследовании непрерывных случайных величин является произведение двух характеристик, так как элемент вероятности F(x)∙dx.

В статистике площадь гистограммы должна быть примерно равна единице.

В распределении Гаусса следует проверить совпадение математического ожидания, моды и медианы.

μ₀=a₀+((∆x(m₀-m₀’))/(2m₀-m₀’-m₀”)), a₀ – начало модального интервала, m₀ – частота модального интервала, m₀’ – частота интервала, предшествующего модальному, m₀” – частота интервала, следующего за модальным.

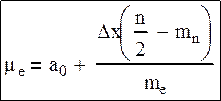
где a₀ – начало медианного интервала, m_n – частота, накопленная к началу медианного интервала и m_e – частота медианного интервала. При анализе критериев согласия следует помнить, что для распределения Гаусса существует три линейных связи.

· Сумма частот равна объему выборки.

· Выравнивающие частоты дают среднее значение равное соответствующей статистике выборки.

· Выравнивающие частоты должны давать основное отклонение равное соответствующей статистике выборки, тогда ν=k-3. Для показательного распределения ν=k-2.

Локальная и интегральная теоремы Лапласа

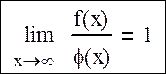Нормальное распределение занимает особое место среди других распределений, так как оно встречается во многих практических задачах. Математики на протяжении длительного времени пытались выяснить причину такого распространения. В 1730 году Муавр нашел асимптотическую формулу для распределения Бернулли при p=0,5. Эта формула позволяет найти вероятность появления ровно k раз в n испытаниях при p=const.

при этом φ(x) является асимптотическим приближением функции f(x). В 1789 Лаплас обобщил формулу Муавра для любого значения p, поэтому теорему иногда называют теоремой Муавра-Лапласа. Муавр доказал, что при n→∞ закон распределения количества появлений события стремится к нормальному.

Существуют локальная и интегральная теоремы Лапласа.