Интегральная теорема

Здесь нужно определить вероятность того, что событие A появится в n испытаниях не менее k₁ и не более k₂ раз:

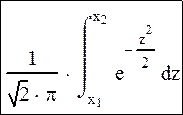p_n(k₁, k₂)≈

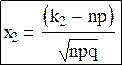
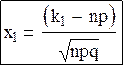
где

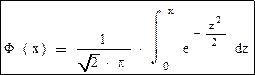Существуют специальные таблицы, в которых указаны значения функции Лапласа или интеграла вероятностей Лапласа:

Φ(-x)=-Φ(x) при x>5 Φ(x)=0,5

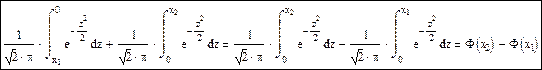Формулу для расчета вероятностей можно получить следующим образом:

p_n(k₁, k₂)≈

Формулу Муавра-Лапласа можно преобразовать. Например,

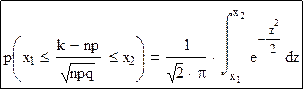
Формулу можно преобразовать к следующему виду:

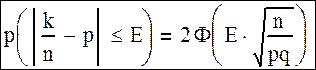
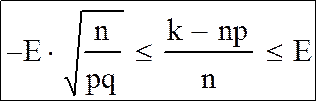Такую формулу можно получить следующим образом:

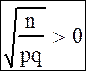Можно умножить неравенство на

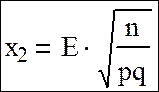
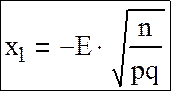
и обозначить

Формула показывает расчет отклонения выборочной вероятности от теоретической на величину сравнимую с малым числом эпсилон.

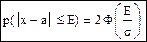Теорема Муавра-Лапласа имеет и другое практическое применение. Можно представить интегральную теорему Лапласа в виде:

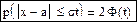Пусть E=σt, где t=1, 2, 3, тогда

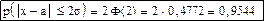При t=2:

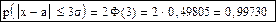При t=3:

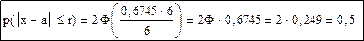С теоремой Лапласа связано также понятие вероятной ошибки: E=r=0,6745∙σ, тогда:

Это значит, что отклонение x от математического ожидания большее, чем r и меньшее, чем r одинаково вероятно.

Таким образом, нормальное распределение Гаусса является предельным случаем биномиального распределения, когда число испытаний неограниченно возрастает, при этом p и q не очень малы. Переход от дискретного биномиального распределения к непрерывному нормальному распределению осуществляется по теореме Муавра-Лапласа. Локальная формула Муавра-Лапласа применяется при обычной вероятности и больших значениях n и m(k). При этом нужно найти определенное значение частоты.

Если вероятность обычная n и m(k) – велики, то нужно найти вероятность попадания в интервал. Тогда используется интегральная формула Муавра-Лапласа. При решении задач n может быть велико, а p малой (меньше 0,01), тогда нужно применять распределение Пуассона.

Закон Пуассона применяется при изучении систем массового обслуживания. В таких системах все потоки событий являются Пуассоновскими. При этом поток событий – это последовательность событий, происходящих одно за другим в некоторые моменты времени. Поток должен быть Марковским, то есть обладать следующими свойствами:

- Стационарности.

- Отсутствие последствия.

- Отсутствие ординарности.

· Характеризуется тем, что вероятность появлений k событий на любом промежутке времени зависит только от числа k и от длительности t этого промежутка и не зависит от начала его отсчета. При этом различные промежутки времени являются непересекающимися.

· Характеризуется тем, что вероятность появления k событий на любом промежутке времени не зависит от того, появились или нет эти события в предшествующие моменты времени, то есть условная вероятность появления k событий на любом промежутке времени равна безусловной вероятности. Состояние потоков в прошлом не меняет их состояния в будущем.

· Характеризуется тем, что появление двух и более событий за малый промежуток времени практически невозможно.

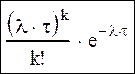Потоки событий, обладающие этими тремя свойствами, и являются простейшими или Пуассоновскими. Потоки могут быть близкими к простейшим. Для таких потоков можно найти вероятность того, что за время τ произойдет ровно k событий. p_k(τ)=

где λτ – математическое ожидание числа событий за время τ. λ – интенсивность потока событий, которая равна среднему числу событий, приходящихся на единицу времени.