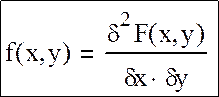 Для непрерывных случайных величин интегральная f(x) всюду непрерывна и имеет непрерывную смешанную частную производную второго порядка:
Для непрерывных случайных величин интегральная f(x) всюду непрерывна и имеет непрерывную смешанную частную производную второго порядка:
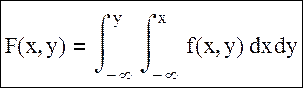 Геометрически это поверхность, которая называется поверхностью распределения. По определению f(x):
Геометрически это поверхность, которая называется поверхностью распределения. По определению f(x):
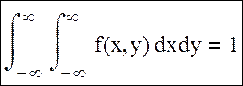 Вероятностный смысл дифференциальной функции двумерной случайной величины: он связан с вероятностью попадания случайной точки в прямоугольник со сторонами δx и δy. Тогда вероятность попадания случайной точки в некоторую произвольную область p((x,y)‹D)=∫∫f(x,y)dxdy, то есть это двойной интеграл по области → (D) от дифференциальной функции. Геометрически это объем тела, ограниченного сверху поверхностью z=f(x,y), а основанием его служит проекция этой поверхности на плоскость (x0,y). Подынтегральное выражение ∫∫f(x, y)dxdy является элементом вероятности. Это вероятность попадания случайной точки в прямоугольник со сторонами dx и dy:
Вероятностный смысл дифференциальной функции двумерной случайной величины: он связан с вероятностью попадания случайной точки в прямоугольник со сторонами δx и δy. Тогда вероятность попадания случайной точки в некоторую произвольную область p((x,y)‹D)=∫∫f(x,y)dxdy, то есть это двойной интеграл по области → (D) от дифференциальной функции. Геометрически это объем тела, ограниченного сверху поверхностью z=f(x,y), а основанием его служит проекция этой поверхности на плоскость (x0,y). Подынтегральное выражение ∫∫f(x, y)dxdy является элементом вероятности. Это вероятность попадания случайной точки в прямоугольник со сторонами dx и dy:

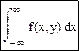 Для каждой составляющей можно определить дифференциальную функцию, используя двумерную плотность вероятности: f1(x)=, f2(x)=
Для каждой составляющей можно определить дифференциальную функцию, используя двумерную плотность вероятности: f1(x)=, f2(x)=
то есть дифференциальные функции одной из составляющих равны несобственному интегралу с бесконечными пределами от дифференциальной функции системы, причем переменная интегрирования соответствует другой составляющей.
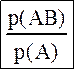 Все рассмотренные характеристики системы связаны с безусловными законами распределения. Кроме них существуют условные законы распределения составляющих. Ранее было доказано, что условная вероятность какого-либо события отличается. PA(B)=
Все рассмотренные характеристики системы связаны с безусловными законами распределения. Кроме них существуют условные законы распределения составляющих. Ранее было доказано, что условная вероятность какого-либо события отличается. PA(B)=
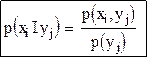 Для системы величин формируется следующее событие: пусть в результате испытания y приняла значение равное yj. При этом x примет одно из своих возможных значений xi. Тогда формируется условная вероятность того, что x примет значение xi при условии, что y примет значение yj:
Для системы величин формируется следующее событие: пусть в результате испытания y приняла значение равное yj. При этом x примет одно из своих возможных значений xi. Тогда формируется условная вероятность того, что x примет значение xi при условии, что y примет значение yj:
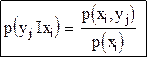 Аналогично рассуждая можно записать, что условное распределение составляющей y при условии, что другая составляющая приняла конкретное значение, имеет вид:
Аналогично рассуждая можно записать, что условное распределение составляющей y при условии, что другая составляющая приняла конкретное значение, имеет вид:
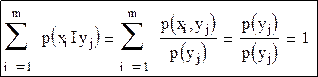 В соответствии с аксиоматикой сумма вероятностей условных распределений равна единице, что можно легко доказать:
В соответствии с аксиоматикой сумма вероятностей условных распределений равна единице, что можно легко доказать:
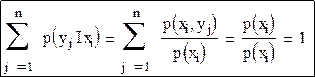
Зная условные законы распределения можно найти условные математические ожидания составляющих.
Для непрерывных случайных величин можно получить закон распределения в виде плотности. Для x: φ(x|y)=f(x,y)/f2(y), для y: ψ(y|x)=f(x,y)/f1(x).
Из этих двух уравнений можно получить закон распределения системы случайных величин: f(x,y)=f2(y)∙φ(x|y)=f1(x)∙ψ(y|x).
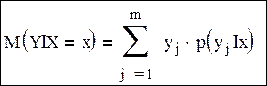 Закон распределения системы случайных величин равен произведению закона распределения одной составляющей на условный закон распределения другой составляющей. Математическое ожидание для дискретных случайных величин:
Закон распределения системы случайных величин равен произведению закона распределения одной составляющей на условный закон распределения другой составляющей. Математическое ожидание для дискретных случайных величин:
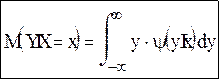 Для непрерывных случайных величин:
Для непрерывных случайных величин:
| y x | x1=1 | x2=2 | x3=3 | Σ |
| y1=3 | 0,1 | 0,3 | 0,2 | 0,6 |
| y2=6 | 0,06 | 0,18 | 0,16 | 0,4 |
| Σ | 0,16 | 0,48 | 0,36 | 1 1 |
Из этой таблицы можно поучить несколько условных законов распределения составляющих.
Для системы двух величин важным параметром, или числовой характеристикой является коэффициент корреляции, или основной момент. Он показывает, являются ли случайные величины зависимыми или независимыми. Случайные величины являются независимыми, если закон распределения одной случайной величины не зависит от того, какие возможные значения принимает другая величина, то есть условные распределения независимых величин равны их безусловным распределениям. По определению независимых случайных величин интегральная функция системы должна быть равна произведению интегральных функций составляющих. Для дискретных случайных величин: F(x, y)=F1(x)∙F2(y). Для непрерывных случайных величин: F(x,y)=f1(x)∙f2(y).
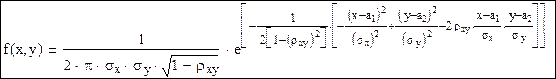 Из-за широкого распространения нормального распределения для системы двух величин можно записать:
Из-за широкого распространения нормального распределения для системы двух величин можно записать:
где a1 и a2 – математические ожидания составляющих, σx и σy – их средние квадратические отклонения, ρxy – коэффициент корреляции.
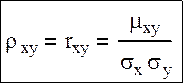 Анализируя формулу можно сделать вывод о том, что ρ изменяется по модулю от 0 до 1. Если ρxy=0, то случайные величины являются независимыми, или некоррелированными. Коэффициент корреляции можно получить по следующей формуле:
Анализируя формулу можно сделать вывод о том, что ρ изменяется по модулю от 0 до 1. Если ρxy=0, то случайные величины являются независимыми, или некоррелированными. Коэффициент корреляции можно получить по следующей формуле:
это отношение корреляционного момента к произведению средних квадратических отклонений двух величин. μxy – это математическое ожидание произведения отклонений случайных величин. Эта характеристика называется ковариацией: μxy=M[(x-Mx)(y-My)].
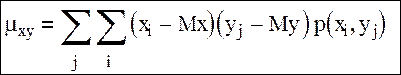 Для дискретных случайных величин:
Для дискретных случайных величин:
Для непрерывных случайных величин:

Для независимых случайных величин μ=0.
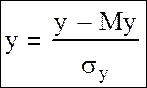
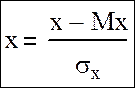 μxy имеет размерность равную произведению размерностей двух случайных величин, то есть зависит от единиц измерения случайных величин, что является недостатком данного параметра. Поэтому он используется, как правило, только при расчете rxy. В формуле двумерной нормально распределенной величины есть две статистики, или нормированные величины:
μxy имеет размерность равную произведению размерностей двух случайных величин, то есть зависит от единиц измерения случайных величин, что является недостатком данного параметра. Поэтому он используется, как правило, только при расчете rxy. В формуле двумерной нормально распределенной величины есть две статистики, или нормированные величины:
Математическое ожидание этих величин стремится к нулю. σ2=1.
Тогда коэффициент корреляции можно найти по формуле:
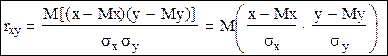
=M(x’y’)=μ(x’y’),
то есть коэффициент корреляции равен корреляционному моменту нормированных величин.
 2015-07-04
2015-07-04 852
852








