2015-07-04
723
Это вероятность события, состоящая в том, что случайная величина x примет значение меньше текущего и при этом вторая составляющая y примет значение меньше другого текущего значения.
F(x,y)=p(X<x, Y<y).
Геометрическая интерпретация интегральной функции заключается в вероятности того, что случайная точка попадет в бесконечный квадрант с вершиной (x,y), расположенный левее и ниже этой вершины.
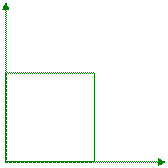y
(x,y)
0 x
Все свойства интегральной F(x) одномерной случайной величины справедливы и для двумерной, например вероятность попадания в интервал заменяется попаданием в полуполосу или в прямоугольник.
· Будем находить вероятность, если x задается интервалом, а y меньше текущего.
p(x1<x< x2, Y<y)
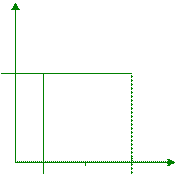
(x1,y) (x2,y)
y
x1 x x2
F(x2,y)=p(X2<x2, Y<y)
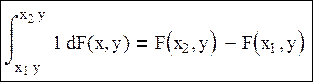
, p(x1y<x<x2y)
· p(X<x, y1< y< y2)
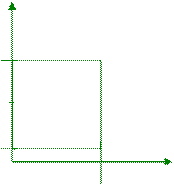
y2 (x,y2)
y
y1 (x,y1)
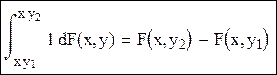
, то есть p((x,y1)<y<(x,y2))
· p(x1< x< x2, y1< y< y2)
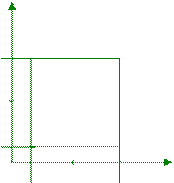
y2 (x1,y2) (x2,y2)
y
y1 (x1,y1) (x2,y1)
x1 x x2
(F(x2,y2)-F(x1,y2))-(F(x2,y1)-F(x1,y1))=F(x2,y2)-F(x1,y2)-F(x2,y1)+F(x1,y1)
Таким образом, вероятность попадания в ту или иную область связана с приращениями интегральной функции распределения.
|
|
|
