Количество функций двух переменных 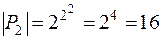 , а для трёх переменных имеем уже
, а для трёх переменных имеем уже 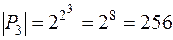 функций.
функций.
Таблицы истинности всех шестнадцати булевых функций двух переменных представлены в табл. 2.3.
Таблица 2.3
| x 1 | x 2 | f 1 | f 2 | f 3 | f 4 | f 5 | f 6 | f 7 | f 8 | f 9 | f 10 | f 11 | f 12 | f 13 | f 14 | f 15 | f 16 |
| Фиктивные переменные | x 1 x 2 | x 2 | x 1 | x 1 | x 2 | x 1 x 2 |
Для каждой функции в четырёх строках таблицы приведены её значения, соответствующие четырём возможным комбинациям аргументов x 1 и x 2 . В таблице для каждой функции показаны также фиктивные переменные, если они имеются.
Функция f 1 называется нулём, а f 16 – единицей, как и в случае функций одной переменной. Функции f 4, f 6, f 11 и f 13 не зависят от одного из аргументов: 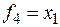 ,
, 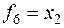 ,
, 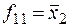 ,
, 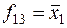 . Для функций f 4 и f 13 переменная x 1 является существенной, а x 2 – несущественной; для функций f 6 и f 11 – всё наоборот.
. Для функций f 4 и f 13 переменная x 1 является существенной, а x 2 – несущественной; для функций f 6 и f 11 – всё наоборот.
|
|
|
Только оставшиеся десять функций являются полноценными нетривиальными функциями двух переменных.
Табл. 2.3 можно представить и в другом виде, выполнив её транспонирование, результатом чего является табл. 2.4, где в последнем столбце указаны также обозначения соответствующих логических операций.
Рассмотрим подробнее все нетривиальные функции двух переменных, а для некоторых из них и функции трёх аргументов. Для функций двух переменных дополнительно проведены иллюстрации, поясняющие смысл соответствующих логических операций.
Таблица 2.4
| Функция | х 1 х 2 | Обозначения функций | |||
| f 1 | “0” | ||||
| f 2 | 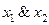 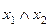 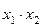 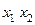 | ||||
| f 3 | 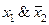 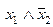 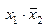 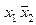 | ||||
| f 4 | x 1 | ||||
| f 5 | 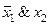 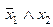 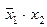 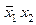 | ||||
| f 6 | x 2 | ||||
| f 7 | 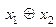 | ||||
| f 8 | 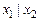 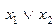 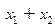 | ||||
| f 9 | 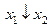 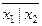 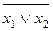 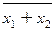 | ||||
| f 10 | 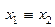 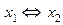 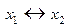 | ||||
| f 11 | 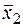 | ||||
| f 12 | 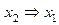 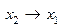 | ||||
| f 13 | 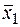 | ||||
| f 14 | 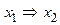 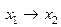 | ||||
| f 15 | 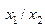 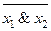 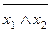 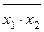 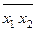 | ||||
| f 16 | “1” |
Функция f 2(x 1, x 2) = 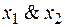 или
или 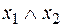 или
или 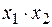 или
или 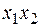 называется конъюнкцией, логическим умножением или функциейИ. Она принимает значение 1 только в том случае, когда все аргументы равны 1 (и x 1 = 1, и x 2 = 1), а значение 0 – во всех остальных случаях (когда хотя бы одна из переменных будет равна 0).
называется конъюнкцией, логическим умножением или функциейИ. Она принимает значение 1 только в том случае, когда все аргументы равны 1 (и x 1 = 1, и x 2 = 1), а значение 0 – во всех остальных случаях (когда хотя бы одна из переменных будет равна 0).
 | x 1 | x 2 | F | x 1 | x 2 | x 3 | F | ||
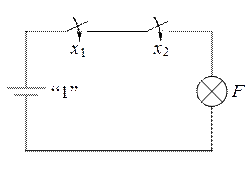
Рис. 2.2. Логическая функция И
|
|
|
На рис. 2.2 поясняется смысл операции И. Видно, что по цепи потечёт ток и лампочка загорится (F = 1) только тогда, когда замкнуты оба ключа (и x 1 = 1, и x 2 = 1).
Функция И трёх и более переменных также принимает значение “1” только при единичных значениях всех её аргументов (и x 1 = 1, и x 2 = 1, и x 3 = 1). Таблица истинности функции И имеет только одну “1” на последней комбинации.
Функция f 8(x 1, x 2) = 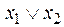 или
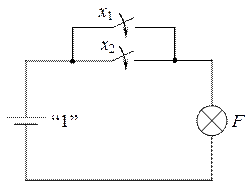
или  называется дизъюнкцией, логическим сложением или функцией ИЛИ. Она принимает значение 1, если хотя бы один из аргументов или все равны 1 (или x 1 = 1, или x 2 = 1, или x 1 = x 2 = 1), а значение 0 – только при x 1 = x 2 = 0. Из рис. 2.3 видно, что по цепи лампочки потечёт ток и она загорится тогда, когда замкнут хотя бы один из ключей.
называется дизъюнкцией, логическим сложением или функцией ИЛИ. Она принимает значение 1, если хотя бы один из аргументов или все равны 1 (или x 1 = 1, или x 2 = 1, или x 1 = x 2 = 1), а значение 0 – только при x 1 = x 2 = 0. Из рис. 2.3 видно, что по цепи лампочки потечёт ток и она загорится тогда, когда замкнут хотя бы один из ключей.
 | x 1 | x 2 | F | x 1 | x 2 | x 3 | F | ||
Рис. 2.3. Логическая функция ИЛИ
Функция ИЛИ трёх и более переменных также принимает значение “1” при единичном значении любого из аргументов (или
x 1 = 1, или x 2 = 1, или x 3 = 1, или x 1 = x 2 = x 3 = 1). Таблица истинности функции ИЛИ имеет только один “0” на первой комбинации.
Функция f 15(x 1, x 2) = 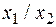 или
или 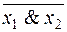 или
или 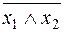 или
или 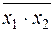 или
или 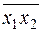 называется штрихом Шеффера, функцией Шеффера или функцией И-НЕ. Она работает полностью противоположно операции И, поэтому принимает значение 0 только в том случае, когда все аргументы равны 1 (и x 1 = 1, и x 2 = 1), а значение 1 – в остальных случаях, т. е. когда хотя бы один из аргументов равен 0.
называется штрихом Шеффера, функцией Шеффера или функцией И-НЕ. Она работает полностью противоположно операции И, поэтому принимает значение 0 только в том случае, когда все аргументы равны 1 (и x 1 = 1, и x 2 = 1), а значение 1 – в остальных случаях, т. е. когда хотя бы один из аргументов равен 0.
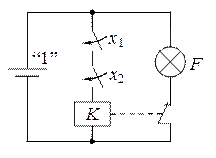
На рис. 2.4 поясняется смысл операции И-НЕ. Видно, что в цепи лампочки не будет течь ток и она не будет гореть (F = 0) только тогда, когда оба ключа замкнуты (и x 1 = 1, и x 2 = 1), т. к. при этом реле K срабатывает и размыкает свой ключ. Если же разомкнут хотя бы один из ключей (или x 1 = 0, или x 2 = 0, или x 1 = x 2 = 0), то реле не размыкает ключ в цепи лампочки и она горит (F = 1).
 | x 1 | x 2 | F | x 1 | x 2 | x 3 | F | ||
Рис. 2.4. Логическая функция И-НЕ
Функция И-НЕ трёх и более переменных также принимает значение “0” только при единичных значениях всех её аргументов (и x 1 = 1, и x 2 = 1, и x 3 = 1). Вообще таблица истинности функции И-НЕ имеет только один “0” на последней комбинации.
Функция f 9(x 1, x 2) = 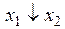 или
или 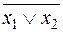 или
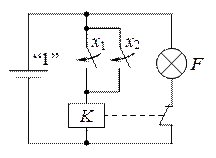
или 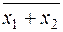 называется функцией Пирса, стрелкой Пирса, а также функцией ИЛИ-НЕ. Она принимает значение 0, если хотя бы один из аргументов или все равны 1 (или x 1 = 1, или x 2 = 1, или x 1 = x 2 = 1), а значение 1 – только при x 1 = x 2 = 0. Из рис. 2.5 видно, что в цепи лампочки не будет течь ток и она не будет гореть (F = 0), если замкнут хотя бы
называется функцией Пирса, стрелкой Пирса, а также функцией ИЛИ-НЕ. Она принимает значение 0, если хотя бы один из аргументов или все равны 1 (или x 1 = 1, или x 2 = 1, или x 1 = x 2 = 1), а значение 1 – только при x 1 = x 2 = 0. Из рис. 2.5 видно, что в цепи лампочки не будет течь ток и она не будет гореть (F = 0), если замкнут хотя бы
 | x 1 | x 2 | F | x 1 | x 2 | x 3 | F | ||
Рис. 2.5. Логическая функция ИЛИ-НЕ
один из ключей (или x 1 = 1, или x 2 = 1, или x 1 = x 2 = 1), т. к. при этом реле K срабатывает и размыкает свой ключ. Если же оба ключа разомкнуты (и x 1 = 0, и x 2 = 0), то реле не размыкает ключ в цепи лампочки и она горит (F = 1).
|
|
|
Функция ИЛИ-НЕ трёх и более переменных также принимает значение “0” при единичном значении любого из аргументов (или x 1 = 1, или x 2 = 1, или x 3 = 1, или x 1 = x 2 = x 3 = 1). Таблица истинности функции ИЛИ имеет только одну “1” на первой комбинации.
Функция f 7(x 1, x 2) = 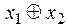 называется функцией сложения по модулю 2, а также исключающим ИЛИ, кольцевой суммой, нетождественностью, неэквивалентностью, нечётностью. Значения этой функции получаются по правилу суммы по модулю 2: 0 Å 0 = 0, 0 Å 1 = 1, 1 Å 0 = 1, 1 Å 1 = 0. Она принимает значение 1, когда только один из аргументов равен 1 (или только x 1 = 1, или только x 2 = 1) или когда сумма значений аргументов является нечётным числом, исключая тем самым одинаковые значения аргументов, т. к. при равных значениях переменных функция принимает значение 0.
называется функцией сложения по модулю 2, а также исключающим ИЛИ, кольцевой суммой, нетождественностью, неэквивалентностью, нечётностью. Значения этой функции получаются по правилу суммы по модулю 2: 0 Å 0 = 0, 0 Å 1 = 1, 1 Å 0 = 1, 1 Å 1 = 0. Она принимает значение 1, когда только один из аргументов равен 1 (или только x 1 = 1, или только x 2 = 1) или когда сумма значений аргументов является нечётным числом, исключая тем самым одинаковые значения аргументов, т. к. при равных значениях переменных функция принимает значение 0.
 | x 1 | x 2 | F | x 1 | x 2 | x 3 | F | ||
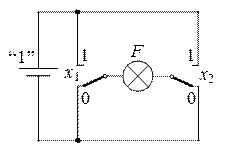
Рис. 2.6. Логическая функция Исключающее ИЛИ
Из рис. 2.6 видно, что в цепи лампочки будет течь ток и она будет гореть (F = 1) только тогда, когда переменные x 1 и x 2 будут иметь различные значения (только в этом случае лампочка будет подключена к батарее). При одинаковых значениях переменных лампочка будет замыкаться сама на себя и не будет гореть (F = 0).
Для трёх и более переменных такая функция будет иметь смысл только функции суммы по модулю 2 (кольцевой суммы) и нечётности. Например, значение функции будет равно 1, если сумма всех значений аргументов есть нечётное число, и 0 – если эта сумма является чётным числом.
Функция f 10(x 1, x 2) = 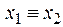 или
или 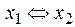 или
или 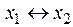 показывает равнозначность (эквивалентность, тождественность) аргументов x 1, x 2 . Она также называется функцией чётности. Эта функция принимает значение 1, только когда оба аргумента равны между собой (или x 1 = x 2 = 0, или x 1 = x 2 = 1) или когда сумма значений аргументов является чётным числом, поэтому можно сделать вывод, что она является обратной функцией для исключающего ИЛИ.
показывает равнозначность (эквивалентность, тождественность) аргументов x 1, x 2 . Она также называется функцией чётности. Эта функция принимает значение 1, только когда оба аргумента равны между собой (или x 1 = x 2 = 0, или x 1 = x 2 = 1) или когда сумма значений аргументов является чётным числом, поэтому можно сделать вывод, что она является обратной функцией для исключающего ИЛИ.
|
|
|
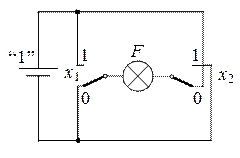 | x 1 | x 2 | F | x 1 | x 2 | X 3 | F | ||
Рис. 2.7. Логическая функция равнозначности (чётности)
Для получения схемы функции равнозначности (чётности) можно на схеме на рис. 2.6 поменять местами контакты любой из переменной, но только одной: либо для x 1 , либо для x 2 .
Из рис. 2.7 видно, что в цепи лампочки будет течь ток и она будет гореть (F = 1) только тогда, когда переменные x 1 и x 2 будут иметь одинаковые значения, т. к. только в этом случае лампочка будет подключена к батарее. При разных значениях переменных лампочка будет замыкаться сама на себя и не будет гореть (F = 0).
Для трёх и более переменных такая функция будет иметь смысл только функции чётности. Например, значение функции будет равно 1, если сумма всех значений аргументов есть чётное число, и 0 – если эта сумма – нечётное число.
Функция f 12(x 1, x 2) = 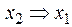 или
или 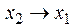 – функция следования (импликация) от x 2 к x 1 , которая принимает значение 0 тогда и только тогда, когда x 1 = 0, а x 2 = 1.
– функция следования (импликация) от x 2 к x 1 , которая принимает значение 0 тогда и только тогда, когда x 1 = 0, а x 2 = 1.
Функция f 14(x 1, x 2) = 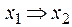 или
или 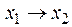 – функция следования (импликация) от x 1 к x 2, принимающая значение 0 тогда и только тогда, когда x 1 = 1, а x 2 = 0.
– функция следования (импликация) от x 1 к x 2, принимающая значение 0 тогда и только тогда, когда x 1 = 1, а x 2 = 0.
В табл. 2.5 и 2.6 отражены таблицы истинности этих двух функций-импликаций, которые имеют смысл только для двух аргументов.
Таблица 2.5 Таблица 2.6
| x 1 | x 2 | F | x 1 | x 2 | F | |
Импликация 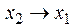 Импликация
Импликация 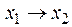
Функция f 3(x 1, x 2) = 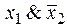 или
или 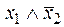 или
или 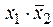 или
или 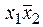 называется функцией запрета по x 2 и характеризуется тем, что равенство x 2 = 1 запрещает функции принимать значение “1” при любых значениях аргумента x 1 , обнуляя тем самым функцию.
называется функцией запрета по x 2 и характеризуется тем, что равенство x 2 = 1 запрещает функции принимать значение “1” при любых значениях аргумента x 1 , обнуляя тем самым функцию.
Функция f 5(x 1, x 2) = 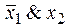 или
или 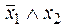 или
или 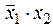 или
или 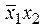 называется функцией запрета по x 1 , т. к. равенство x 1 = 1 запрещает функции принимать значение “1” при любых значениях аргумента x 2 .
называется функцией запрета по x 1 , т. к. равенство x 1 = 1 запрещает функции принимать значение “1” при любых значениях аргумента x 2 .
Таблица 2.7 Таблица 2.8
| x 1 | x 2 | F | x 1 | x 2 | F | |
| 0 | ||||||
| 0 | ||||||
| 0 | 0 |
Функция запрета по x 2 Функция запрета по x 1
Эти две функции запрета, таблицы истинности которых приведены в табл. 2.7 и 2.8, также существуют только для случая двух переменных.
Теоретически, функции И, ИЛИ, И-НЕ, ИЛИ-НЕ, чётность и нечётность могут иметь сколько угодно, но конечное число аргументов x 1, x 2, …, xm.
 2015-07-04
2015-07-04 7989
7989
