Расширение понятия логической функции

Функция f (x ₁ , x ₂ , …, x_m) логических переменных (аргументов) x ₁ , x ₂ , …, x_m, которая также как и переменные может принимать значения только из набора {0, 1}, называется логической (переключательной, булевой) функцией [3].

Как и во всей математике, функция по сути также является переменной, значения которой зависят от других переменных (её аргументов).

Логические функции обозначаются обычно через y или F и записываются в виде

y = f (x ₁ , x ₂ , …, x_m) или F = f (x ₁ , x ₂ , …, x_m), (2.1)

или в виде отображения

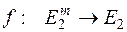, (2.2)

где E ₂ = {0, 1} – конечное множество, состоящее из двух элементов 0 и 1; 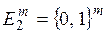– множество m -мерных векторов, составленных из m логических переменных. Значения этих векторов называются также двоичными наборами (комбинациями).

Таким образом, запись вида (2.2) обозначает, что каждому значению m -мерного вектора из {0, 1} ^m или соответствующего набора однозначно ставится в соответствие значение y 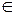{0, 1}.

Булевы функции определены на конечном множестве аргументов, каждый из которых принимает только два значения: 0 или 1. Поэтому булевы функции можно представить таблицей истинности, в которой перечисляются значения функции для каждого набора значений аргументов.

Несмотря на то, что количество булевых функций от любого заданного числа m логических переменных конечно, их слишком много, чтобы иметь запас преобразователей для любых встретившихся отображений. Поэтому основной задачей теории булевых функций является разработка систематического метода построения сложных функций из более простых.

В таблице истинности, описывающей булеву функцию, имеется k = 2 ^m строк, соответствующих различным наборам значений аргументов. Этим k строкам можно сопоставить 2 ^k различных столбцов, соответствующих различным функциям. Таким образом, число булевых функций N от m переменных с ростом m растёт весьма быстро:

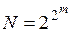. (2.3)

Множество булевых функций от m аргументов обозначается через P_m , также пишут, что N = | P_m |.

Говорят, что булева функция 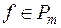существенно зависит от переменной x_i , если существует такой набор значений 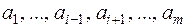, что

.

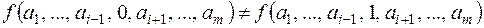В этом случае x_i называют существенной переменной, в противном случае x_i называют несущественной (фиктивной) переменной.

Пример 2.1. Пусть булевы функции f ₁(x ₁, x ₂) и f ₂(x ₁, x ₂) заданы следующими таблицами истинности (табл. 2.1).

Для этих функций f ₁(0, 0) = f ₁(0, 1) = 0 и f ₁(1, 0) = f ₁(1, 1) = 1, f ₂(0, 0) = f ₂(0, 1) = 1 и f ₂(1, 0) = f ₂(1, 1) = 0, поэтому переменная x ₁ – существенная, а переменная x ₂ – несущественная. Как видно из таблицы, 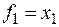и 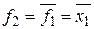, где чёрточка над переменной означает её логическое отрицание.

Две функции могут иметь различные логические выражения, но быть равными. По определению две булевы функции равны (тождественны, эквивалентны), если одна получается из другой введением (или удалением) несущественных переменных. Естественно, у равных функций будут одинаковые таблицы истинности. Поэтому иногда для определения тождественности функций проще выполнить сравнение их таблиц истинности, чем преобразование их логических выражений, по крайней мере первый способ является наиболее достоверным.

Логическая функция называется тривиальной, если она всегда принимает постоянное значение (является константой) или равна одной из своих переменных. В противном случае функция называется нетривиальной.

Тривиальная (т. е. простая, элементарная, примитивная, неоригинальная) функция – это такая функция, понимание которой не требует никаких объяснений.