Модель вида
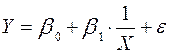 (71)
(71)
называется обратной моделью. Эта модель сводится к линейной заменой 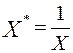 . Данная модель обычно применяется в тех случаях, когда неограниченное увеличение объясняющей переменной
. Данная модель обычно применяется в тех случаях, когда неограниченное увеличение объясняющей переменной 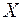 асимптотически приближает зависимую переменную
асимптотически приближает зависимую переменную 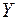 к некоторому пределу (в данном случае к
к некоторому пределу (в данном случае к 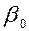 ). В зависимости от знаков
). В зависимости от знаков 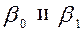 возможны различные ситуации. Если
возможны различные ситуации. Если 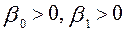 , то (71) может отражать зависимость между объемом выпуска (
, то (71) может отражать зависимость между объемом выпуска (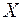 ) и средними фиксированными издержками (
) и средними фиксированными издержками (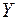 ). Если
). Если 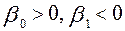 , то (71) может отражать зависимость между доходом
, то (71) может отражать зависимость между доходом 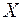 и спросом на блага
и спросом на блага 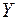 (например, на товары первой необходимости либо товары относительной роскоши); это так называемые функции Торнквиста (в этом случае
(например, на товары первой необходимости либо товары относительной роскоши); это так называемые функции Торнквиста (в этом случае 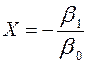 — минимально необходимый уровень дохода). Если
— минимально необходимый уровень дохода). Если 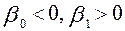 , то получим кривую Филипса, отражающую зависимость между уровнем безработицы (
, то получим кривую Филипса, отражающую зависимость между уровнем безработицы (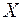 ) в процентах и процентным изменением заработной платы (
) в процентах и процентным изменением заработной платы (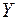 ). При этом точка пересечения кривой с осью ОХ определяет естественный уровень безработицы.
). При этом точка пересечения кривой с осью ОХ определяет естественный уровень безработицы.
Рассмотрим пример 7. Имеются данные по 10 семьям о доходе 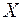 (ден. ед.) и потреблении некоторого продукта
(ден. ед.) и потреблении некоторого продукта 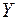 (кг) (табл. 8).
(кг) (табл. 8).
|
|
|
Таблица 8.
| Семья | 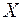
| 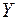
| 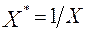
|
| 5,6 | 1,0 | ||
| 10,8 | 0,5 | ||
| 11,1 | 0,3333 | ||
| 12,1 | 0,25 | ||
| 0,2 | |||
| 14,2 | 0,1667 | ||
| 12,9 | 0,1429 | ||
| 14,1 | 0,125 | ||
| 13,4 | 0,1111 | ||
| 13,7 | 0,1 |
Исходные данные показаны на рис 6,а. Из рисунка видно, зависимость нелинейная. Предположим, что точная зависимость имеет может быть описана уравнением
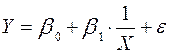
или в линеаризованном виде
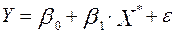 .
.
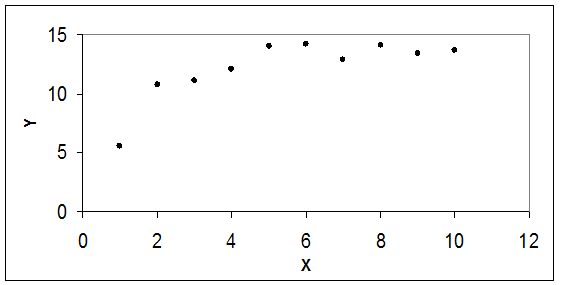
Рис. 6,а. Зависимость потребления Y от дохода X.
График с новыми переменными показан на рис 6, б.
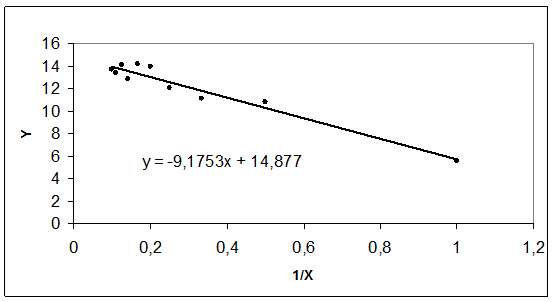
Рис. 6, б. Зависимость потребления Y от величины 1/X.
Коэффициенты линейного уравнения определяются обычным методом наименьших квадратов. Эмпирическое уравнение регрессии имеет вид 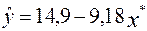 или возвращаясь к исходным переменным получим
или возвращаясь к исходным переменным получим 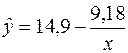 .
.
 2015-07-04
2015-07-04 1682
1682








