Показатели тесноты связи нелинейной регрессии (индекс корреляции и индекс детерминации)

Уравнение нелинейной регрессии, так же, как и в случае линейной зависимости, дополняется показателем тесноты связи. В данном случае это индекс корреляции:

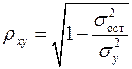, (1.21)

где 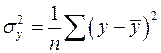– общая дисперсия результативного признака 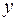, 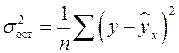– остаточная дисперсия.

Величина данного показателя находится в пределах: 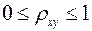. Чем ближе значение индекса корреляции к единице, тем теснее связь рассматриваемых признаков, тем более надежно уравнение регрессии.

Квадрат индекса корреляции носит название индекса детерминации и характеризует долю дисперсии результативного признака 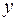, объясняемую регрессией, в общей дисперсии результативного признака:

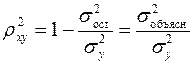, (1.22)

т.е. имеет тот же смысл, что и в линейной регрессии; .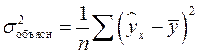

Индекс детерминации 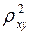можно сравнивать с коэффициентом детерминации 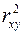для обоснования возможности применения линейной функции. Чем больше кривизна линии регрессии, тем величина 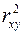меньше 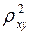. А близость этих показателей указывает на то, что нет необходимости усложнять форму уравнения регрессии и можно использовать линейную функцию.

Индекс детерминации используется для проверки существенности в целом уравнения регрессии по 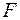-критерию Фишера:

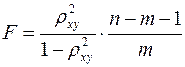, (1.23)

где 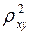– индекс детерминации, 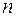– число наблюдений, 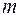– число параметров при переменной 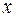. Фактическое значение 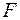-критерия (1.23) сравнивается с табличным при уровне значимости 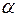и числе степеней свободы 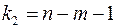(для остаточной суммы квадратов) и 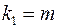(для факторной суммы квадратов).

О качестве нелинейного уравнения регрессии можно также судить и по средней ошибке аппроксимации, которая, так же как и в линейном случае, вычисляется по формуле.