2015-05-10
849
Для оценки значимости уравнения регрессии в целом используется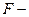 
тест.
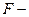тест – оценивание качества уравнения регрессии – состоит в проверке нулевой гипотезы 
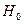о статистической незначимости уравнения регрессии и показателя тесноты связи.
Для этого выполняется сравнение фактического или наблюдаемого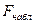 
и критического или табличного 
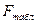значений 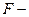критерия Фишера.
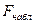определяется из соотношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы:
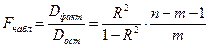. (16)
Здесь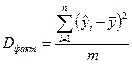 
– факторная сумма квадратов, приходящаяся на одну степень свободы, 
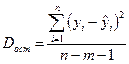– остаточная сумма квадратов, приходящаяся на оду степень свободы, 
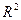– коэффициент (индекс) множественной детерминации, 
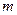– число параметров при переменных 
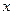(в линейной регрессии совпадает с числом включенных в модель факторов), 
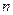– число наблюдений.
Значение 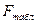определяем из таблицы значений 
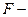критерия Фишера при уровне значимости 
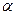и степенях свободы 
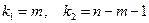. Здесь 
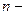объем выборочных данных, 
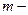число объясняющих переменных в уравнении регрессии. Нулевая гипотеза 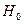принимается на уровне значимости 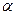, если 
.
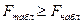Для оценки статистической значимости найденных МНК параметров уравнения регрессии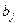 
используется 
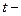тест. Выдвигается нулевая гипотеза 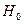о статистической незначимости, то есть случайной природе показателей. Фактические (наблюдаемые) значения 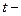критериев находят по формулам:
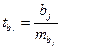(17)
где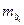 
– средняя квадратическая ошибка коэффициента регрессии 
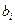, она может быть определена по следующей формуле:
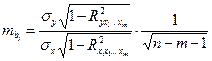(18)
Наблюдаемые значения 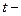критериев сравнивают с критическим значением 
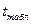, определяемым по таблице Стьюдента по заданному уровню значимости 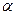и по числу степеней свободы 
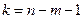. Нулевая гипотеза 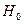отклоняется на уровне значимости 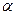, если 
.
ПОСТАНОВКА ЗАДАЧИ
В таблице представлены данные предприятий: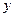 
– фондоотдача, 
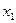– среднечасовая производительность печей, 
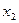– удельный вес активной части основных производственных фондов (числа условные).
| номер наблюдения, i | y | x1 | x2 |
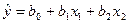.коэффициент детерминации.коэффициентов корреляции. Исследуйте модель на наличие мультиколлинеарности между объясняющими переменными. критерия на уровне 0,05. критерия на уровне 0,05.экономический смысл имеют коэффициенты регрессии. 
