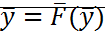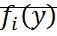Исследование качественной структуры окрестности состояния равновесия (особые точки)

, – компоненты вектора f зависимы от фазовых координат. n=2

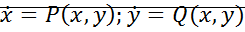
Все первые производные равны 0. 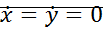; ; 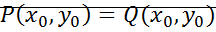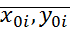– не одна особая точка. Введем обозначения:

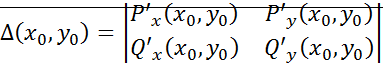
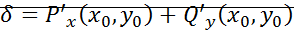. Состояние равновесия в котором 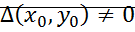наз. простым.

Разложение по степеням нелинейной функции исходного уравнения. :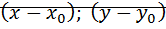

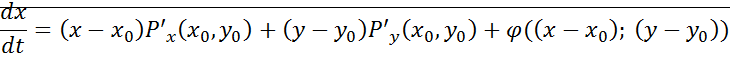
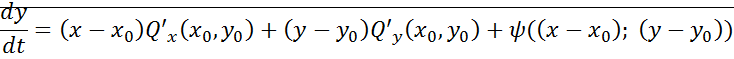
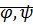– разложение со второго порядка и выше.

Сделаем замену переменных: =>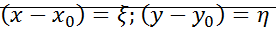

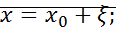
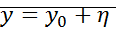
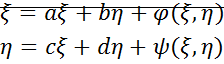
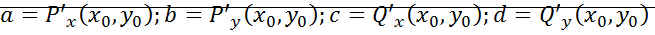
Линеаризация уравнения вблизи 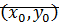: линеаризованная система вблизи точек равновесия.

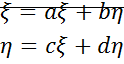
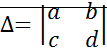
Для системы «хищник-жертва»

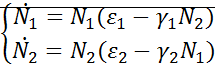
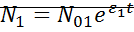
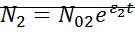
Рассмотрим координаты особых точек:

1. ;

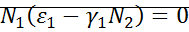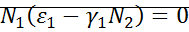
I. (0,0) II. ()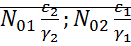

Линеаризация вблизи особых точек:

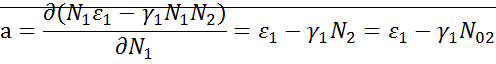
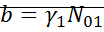
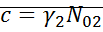
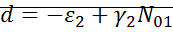
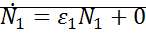
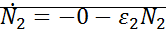
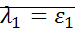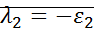; ; (седло)

Поведение системы при больших N

;

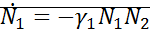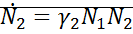
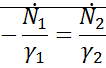
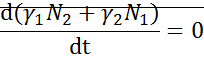
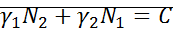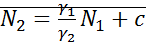-> . Далеко от начала координат имеет прямую.

;

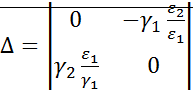
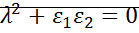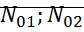
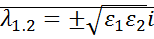
Точка (0,0) – седло.

Сепаратрисы – кривые, проходящие через общую точку

Домножаем уравнения на 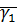и 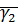, сложим.

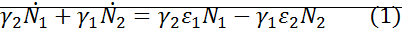
Домножая исходное уравнение на 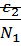и 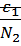и суммируем:

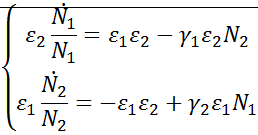
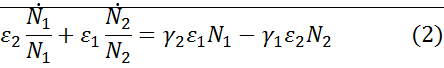
Из (1) вычтем (2):

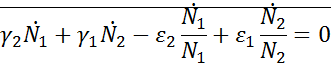
Умножим на dt и проинтегрируем:

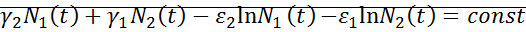
Это выражение будет первым интегралом исходной системы.