Теорема Гурвица

Необходимым и достаточным условием отрицательности всех действительных частей характеристического полинома: 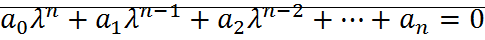с действительными коэффициентами всех главных диагональных миноров матрицы Гурвица.

- Матрица Гурвица

Нечетные столбцы из нечетных коэффициентов. Четные – из четных.

Если вещественные части корней меньше нуля полинома 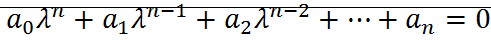, то все коэффициенты больше 0.

Необходимые условия устойчивости системы.

14. Второй метод Ляпунова.

Дана система уравнений:

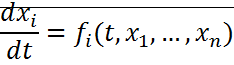
если существует дифференциальная функция называемая функцией Ляпунова 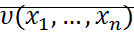, удовлетворяющая в окрестности начала координат следующим условиям:

1. 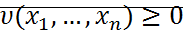, причем 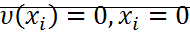. Функция имеет строгий минимум в начале координат

2.

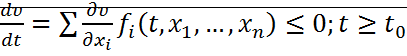
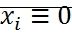– точка покоя – устойчива.

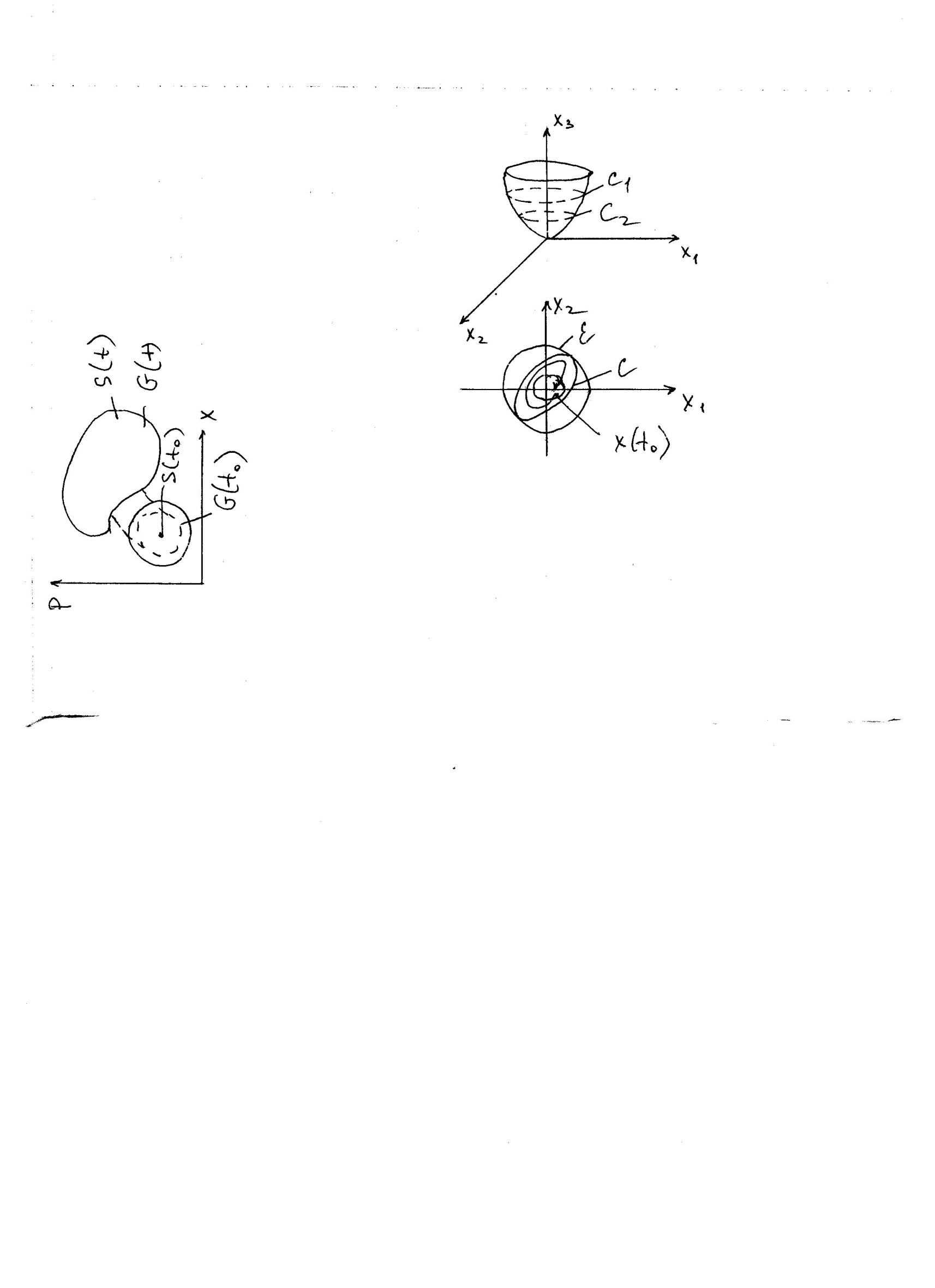В окрестности точки строгого минимума , поверхности линии замкнуты, внутри лежит точка (0,0). Зададим , при достаточно малом C>0, лежит внутри 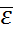, но при этом она проходит через точку 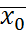. Можно выбрать такое 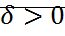, что окрестность начала координат лежит поверхности 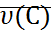, причем 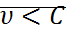, если 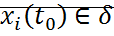, и следовательно 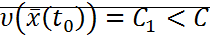, точка траектории, определяемая этими начальными условиями, не может выйти за пределы поверхности 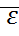, и даже за пределы 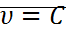, так как по второму условию теоремы 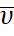– скорость вдоль траектории не возрастает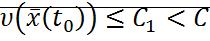

15. Функция Ляпунова.

Дана система уравнений:

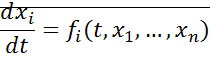
если существует дифференциальная функция называемая функцией Ляпунова 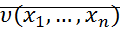, удовлетворяющая в окрестности начала координат следующим условиям:

1. 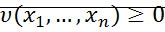, причем 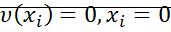. Функция имеет строгий минимум в начале координат

2. t wx:val="Cambria Math"/><w:i/><w:sz w:val="36"/><w:sz-cs w:val="36"/><w:lang w:val="EN-US"/></w:rPr><m:t>t</m:t></m:r></m:e><m:sub><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="36"/><w:sz-cs w:val="36"/></w:rPr><m:t>0</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">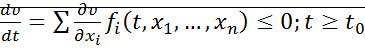

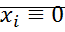– точка покоя – устойчива.

Уточнение к функции Ляпунова.

1. Если 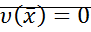только в точке 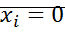и во всей рассматриваемой области она сохраняет один и тот же знак, она называется знакоопределенной, она может быть положительной или отрицательной.

2. Если 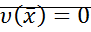не только в точке 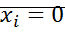, то такая функция знакопостоянная.

3. 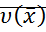- знакопеременная, если в рассматриваемой области не сохраняет одного и того же знака.

Пример: 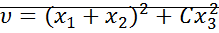– знакопостоянная в т.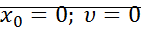

Рассмотрим подробно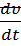

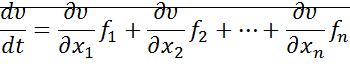
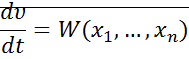
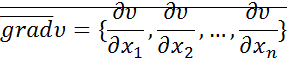
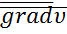– Определен проекциями 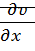на оси координат. 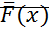- вектор с проекциями на оси координат, .

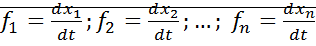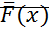- вектор скорости изображения точки m в фазовом пространстве.

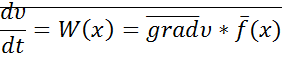
Производная функции Ляпунова, составленная в силу уравнения системы, есть скалярное произведение .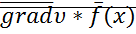

Если 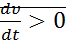, то согласно 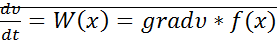угол между фазовой скоростью и градиентом меньше 90 градусов, т.е. фазовая траектория, пересекает поверхность в сторону увеличения .

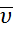Если 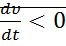, угол между фазовой скоростью и градиентом больше 90 градусов, и фазовая траектория идет в сторону уменьшения .

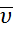Устойчивость: Если для системы уравнений существует знакоопределенная функция 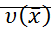, производная которой 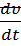является знакопостоянной противоположного знака, то решение системы устойчиво при .

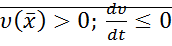, тогда фазовые траектории пересекают С из вне во внутрь 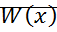, точка может остаться.

Асимптотическая устойчивость: Если для системы дифференциальных уравнений существует знакоопределенная функция 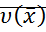, 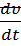тоже знакоопределенная, но противоположного знака, то решение 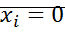- устойчиво асимптотически, при этих условиях фазовая траектория пересекает С не может остаться на поверхности.

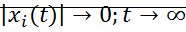
Теорема Ляпунова о неустойчивости: Если для системы дифференциальных уравнений существует 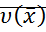, у которой 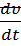- знакоопределенная функция, причем в любой сколь угодно малой окрестности начала координат имеется область в которой знак 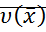совпадает

с 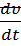, то решение системы 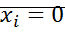неустойчиво.