
При анализе устойчивых предельных циклов можно сделать следующие выводы:
1. В системе устанавливаются незатухающие колебания
2. Амплитуда и частота колебаний не зависят от начальных условий, зависят только от параметров системы.
 Пример: Генератор Ван-Дер-Поля
Пример: Генератор Ван-Дер-Поля
Триод – электронная лампа
 Вольт – амперная характеристика
Вольт – амперная характеристика
S – крутизна.
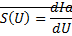
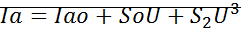 – разложение в ряд
– разложение в ряд
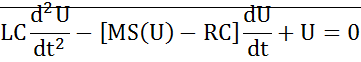
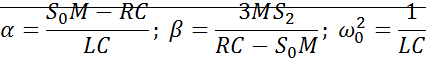
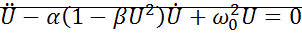
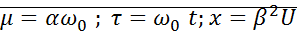
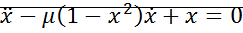 – уравнение Ван-Дер-Поля.
– уравнение Ван-Дер-Поля.
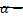 характеризует самовозбуждение
характеризует самовозбуждение
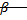 характеризует амплитуду автоколебаний
характеризует амплитуду автоколебаний
Запишем систему
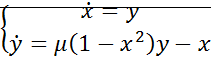 ;
; 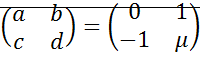 ;
; 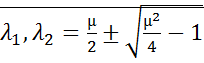
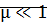 – неустойчивый фокус
– неустойчивый фокус
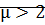 ;
; 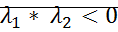 – неустойчивый узел
– неустойчивый узел

9. Приближённый метод исследования предельных циклов. Определение гладкого цикла.
Приближенный метод.
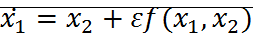
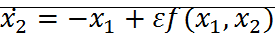
При 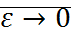 и малых t можно аппроксимировать решение
и малых t можно аппроксимировать решение
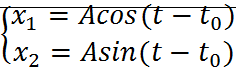
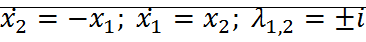
Для линейного осциллятора:
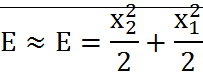
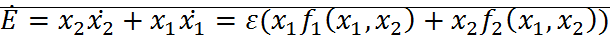
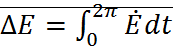 ;
; 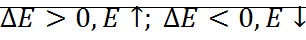
Для уравнения Ван-Дер-Поля.
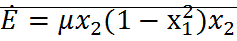
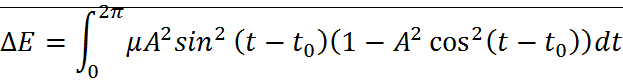
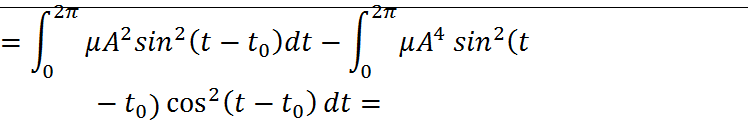
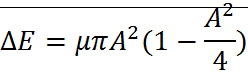
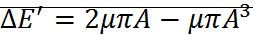 ;
; 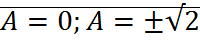 ;
; 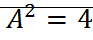 ; A=cosnt;
; A=cosnt; 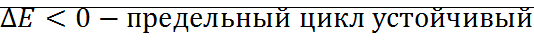

Гладким циклом однократного пресечения называется простая, гладкая, замкнутая кривая С, обладающая следующими свойствами:
1. На кривой С не лежит не одного состояния равновесия
2. Во всех точках кривой С, траектория не имеет с ней касания, и либо входят внутрь, либо выходят.
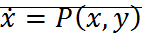
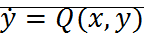
Теорема: Пусть С – цикл однократного пересечения, G – ограниченная им область, принадлежащая области определения системы 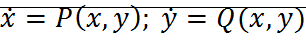 , если
, если
1. Все траектории, пересекающие С при возрастании t входят в G.
2. В области G есть единственное состояние равновесия т.О, являющаяся неустойчивым узлом или фокусом.
10. Критерий Бендиксона.
Отсутствие предельных циклов.
Если в области G выражение 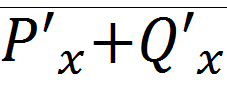 не меняет знак и не равно 0 тождественно, то в этой области не существует замкнутых контуров, составленных из траекторий.
не меняет знак и не равно 0 тождественно, то в этой области не существует замкнутых контуров, составленных из траекторий.
11. Функции последования. Условия устойчивости неподвижной точки точечного преобразования.
На фазовой плоскости возьмем отрезок АВ (дуга без контакта, на ней нет особых точек и фазовые траектории не являются ее касательными) АВ – параметрическая дуга, где 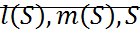 – параметры.
– параметры.
Обозначим через S координату пересечения АВ с фазовой траекторией. С увеличением t, Q опять пересеет АВ, в точке S’.
Точка Q’ (первого следующего пересечения АВ той же фазовой траектории) последующая к исходной т.Q.
Зависимость S’=f(S) соответствующей фазовой траектории в силу решения уравнения 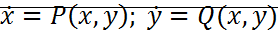 называется функцией последования. Она определена законом точечного преобразования для данной нелинейной системы.
называется функцией последования. Она определена законом точечного преобразования для данной нелинейной системы.
Для функции последования справедливо следующее:
1. Функция последования для аналитической системы, при этом 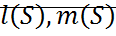 тоже аналитические функции, то и функция последования тоже аналитическая.
тоже аналитические функции, то и функция последования тоже аналитическая.
2. Производная от функции последования всегда >0. Из за того, что траектории не пересекаются.
Возможен случай, что Q’ совпадет с Q.
f(S)=S=S* Получаем замкнутую фазовую траекторию (предельный цикл или кривая соответствует точке центр) Lo.
Рассмотрим последовательно точки пересечения другой траектории L (S1,S2…Sn):
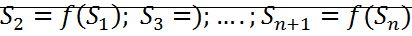
Если 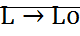 ,
, 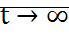 , то последовательность (S1,S2…Sn)
, то последовательность (S1,S2…Sn) 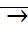 S*
S*
Неподвижная точка S* - отображение S’=f(S), называется устойчивой, если существует такая ее окрестность, что все последовательности (S1,S2…Sn) с начальным условием S1 будут стремится к S’.
Наличие устойчивых или неустойчивых последовательностей (S1,S2…Sn) говорит о наличие устойчивого или неустойчивого предельного цикла.
Условие устойчивости неподвижной точки точечного изображения. (Диаграмма Ламмерея)
Неподвижная точка изображения устойчива, если 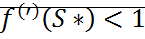 и не устойчива, если
и не устойчива, если 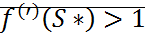

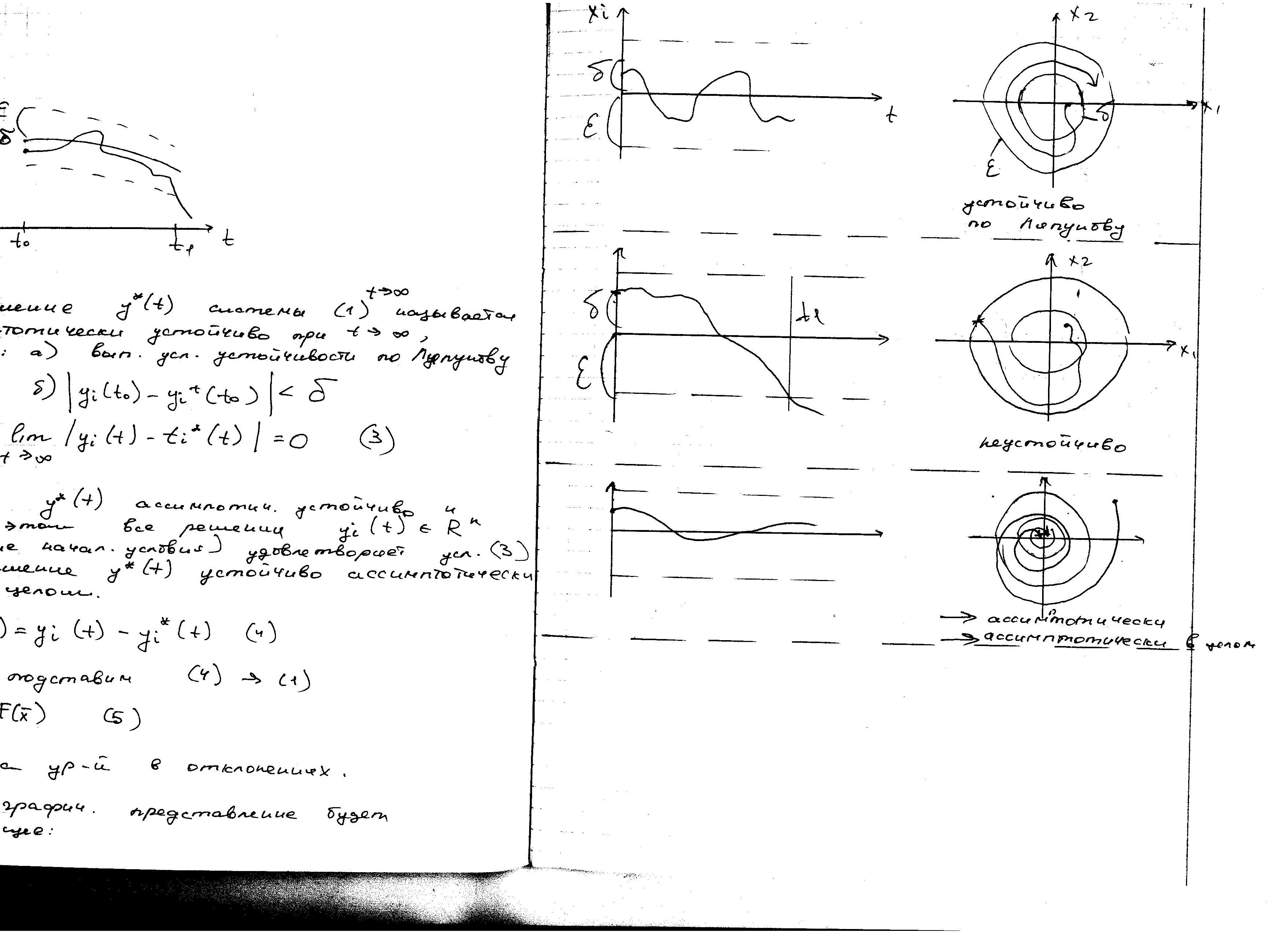
12. Устойчивость решений ДУ. Определение разных типов устойчивых решений ДУ.
Дана система:
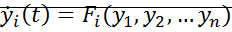
Устойчивость как свойство свободного изменения решения системы после начального отклонения в т. t0.
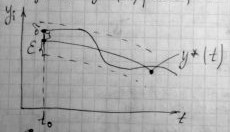
1. Пусть 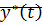 – устойчивое решение, тогда определение устойчивости по Ляпунову.
– устойчивое решение, тогда определение устойчивости по Ляпунову.
Решение 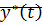 системы нелинейных уравнений будет устойчивым на интервале
системы нелинейных уравнений будет устойчивым на интервале 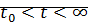 , если при заданном
, если при заданном 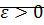 сколько мало бы оно не было, существует
сколько мало бы оно не было, существует  зависящая от
зависящая от 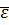 в общем случае, что при начальных условиях:
в общем случае, что при начальных условиях:
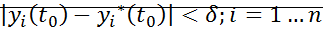
для 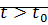 выполняется условие
выполняется условие
Если условие выполняется, то решение устойчиво по Ляпунову.
На фазовой плоскости:
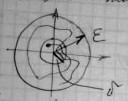
2. Если выходит из области 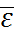 , т.е. условие нарушается, то система неустойчива по Ляпунову.
, т.е. условие нарушается, то система неустойчива по Ляпунову.
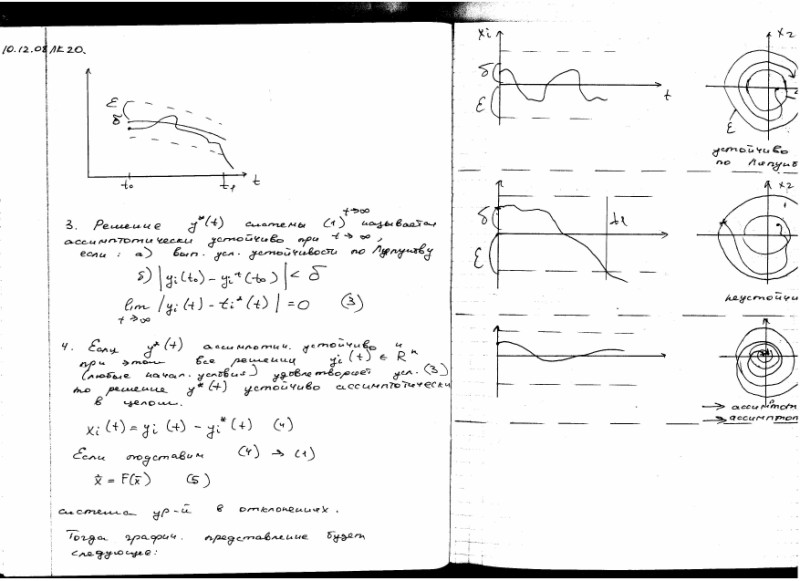
3. Решение 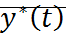 системы
системы 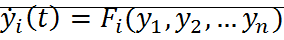
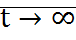 называется асимптотически устойчиво при
называется асимптотически устойчиво при 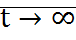 , если:
, если:
а. выполняется условие устойчивости по Ляпунову
б. 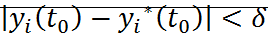 ;
; 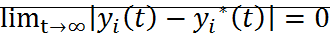
4. Если 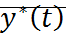 асимптотически устойчиво и при этом все решения
асимптотически устойчиво и при этом все решения 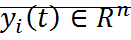 (любые начальные условия) удовлетворяет условию
(любые начальные условия) удовлетворяет условию 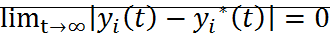 , то решение
, то решение 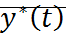 устойчиво асимптотически в целом.
устойчиво асимптотически в целом.
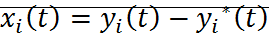
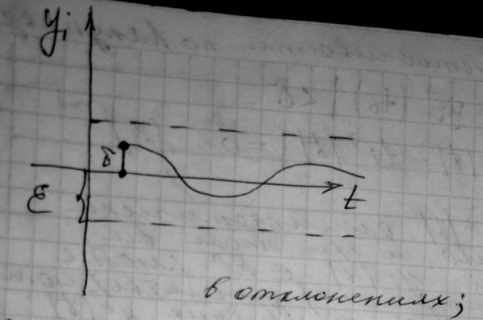
Если подставим 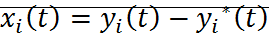 в
в 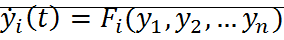 :
: 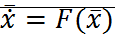 – система уравнений в отклонениях.
– система уравнений в отклонениях.
Тогда графическое представление будет следующее:
13. Корневой критерий устойчивости. Критерий Гурвица.
Для вывода устойчива система или нет, достаточно знать значения корней характеристического уравнения. Линейная система с постоянной матрицей А устойчива тогда и только тогда, когда все 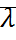 имеют неположительную вещественную часть.
имеют неположительную вещественную часть.
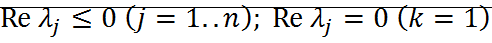
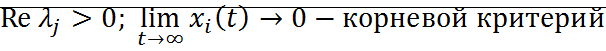
 2015-07-04
2015-07-04 1690
1690
