Замечания

Классическая формулировка Ц.П.Т.

Пусть 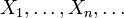есть бесконечная последовательность независимых одинаково распределённых случайных величин, имеющих конечное математическое ожидание и дисперсию. Обозначим последние μ и σ², соответственно. Пусть 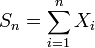. Тогда

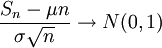по распределению при ,

где N (0,1) — нормальное распределение с нулевым математическим ожиданием и стандартным отклонением, равным единице. Обозначив символом 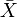выборочное среднее первых n величин, то есть 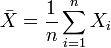, мы можем переписать результат центральной предельной теоремы в следующем виде:

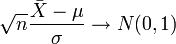по распределению при .

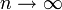Замечания

§ Неформально говоря, классическая центральная предельная теорема утверждает, что сумма n независимых одинаково распределённых случайных величин имеет распределение, близкое к N (n μ, n σ²). Эквивалентно, 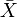имеет распределение близкое к N (μ,σ² / n).

§ Так как функция распределения стандартного нормального распределения непрерывна, сходимость к этому распределению эквивалентна поточечной сходимости функций распределения к функции распределения стандартного нормального распределения. Положив 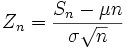, получаем 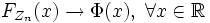, где Φ(x) — функция распределения стандартного нормального распределения.

§ Центральная предельная теорема в классической формулировке доказывается методом характеристических функций (теорема Леви о непрерывности).

§ Вообще говоря, из сходимости функций распределения не вытекает сходимость плотностей. Тем не менее в данном классическом случае имеет место.