2015-07-04
1038
На нелинейное сопротивление с ВАХ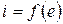 
подается напряжение сигнала 
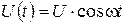, спектр которого известен. Определить спектральный состав тока 
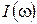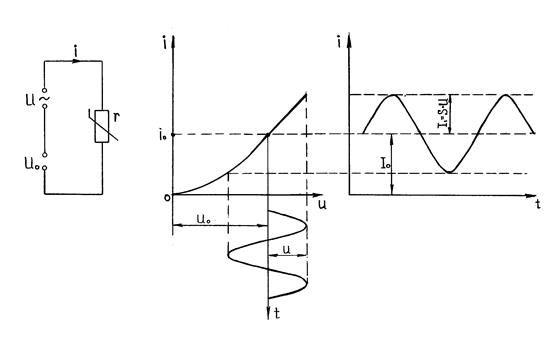
, протекающего в цепи с нелинейным элементом (Н. Э.). Пусть в цепь включено также постоянное смещение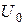 
(рисунок 6. 7, а). Вследствие нелинейности вольт-амперной характеристики форма тока будет отличаться от гармонической. Представим периодическую функцию 
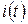в виде ряда Фурье:
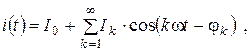
где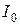 
–– постоянная составляющая тока;
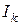–– амплитуды гармоник;
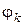–– фаза гармоник.
Ток, протекающий через цепь с нелинейным элементом, содержит высокочастотные составляющие, которые являются следствием проявления нелинейности. Если бы вольт-амперная характеристика была линейна, то высших гармоник (при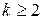 
) не было бы. Таким образом, нелинейные элементы обладают свойством преобразования частоты входного сигнала, которое заключается в том, что в нелинейных устройствах спектр выходного сигнала содержит новые гармоники, которых нет у входного сигнала (воздействия).
Расчет составляющих тока при заданных амплитуде напряжения U и напряжения смещения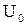 
можно выполнить различными методами. Рассмотрим два из них:
1) метод степенного полинома;
2) метод кусочно-линейной аппроксимации.
|
|
|
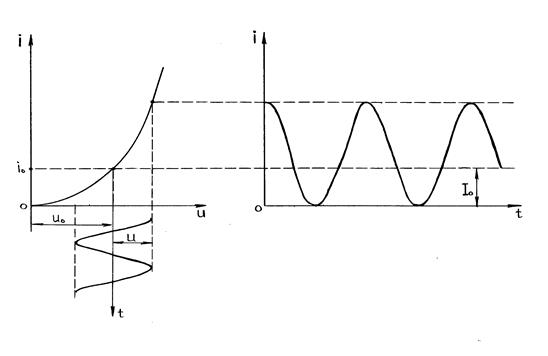
Рисунок 6. 7
Расчет составляющих тока при заданных амплитудах напряжения U и напряжения смещения 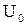можно выполнить различными методами. Рассмотрим два из них:
1) метод степенного полинома;
2) метод кусочно-линейной аппроксимации.
