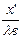В ряде случаев оказывается полезным в первом приближении рассматривать длинную линию как линию, не имеющую потерь, т.е. пренебрегать активным сопротивлением и проводимостью по сравнению с соответствующими реактивными величинами. Отметим здесь, что в реальных цепях с распределенными параметрами довольно часто имеет место ωL 0>> R 0 и ωC 0>> G 0.
Итак, положим R0=G0=0. В этом случае для коэффициента распространения получим:
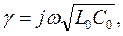 при этом
при этом 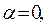
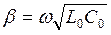 .
.
Волновое сопротивление становится действительной величиной 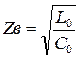 , а фазовая скорость определяется только первичными параметрами линии
, а фазовая скорость определяется только первичными параметрами линии 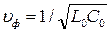 и отсутствует её зависимость от частоты.
и отсутствует её зависимость от частоты.
С учетом этого уравнения (1.24) можно представить в следующем виде:
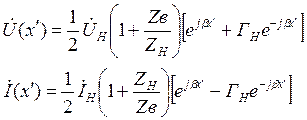 (1.33)
(1.33)
и, соответственно, уравнения передачи длинной линии (1.28)
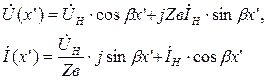 (1.34)
(1.34)
Как видно из уравнения (1.33) распределение напряжений и токов в длинной линии без потерь в значительной степени, определяется величиной ГН, которая в свою очередь зависит от соотношения волнового сопротивления и сопротивления нагрузки. Рассмотрим наиболее характерные случаи режима работы длинной линии без потерь.
Режим согласования. Этот режим работы линии характеризуется равенством сопротивления нагрузки и волнового сопротивления линии, т.е. ZН=Zв. В этом случае в соответствии с (1.25) ГН= 0, что свидетельствует об отсутствии отраженной волны. Тогда, из (1.33) следует:
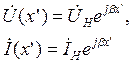
Переходя к мгновенным (временным) значениям тока и напряжения, получаем:
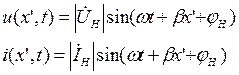
где φН – фаза напряжения и тока в нагрузке (ZН - действительная величина).
Таким образом, в линии без потерь в режиме согласования (или режиме согласованной нагрузки) существует только падающая бегущая волна напряжения и тока, амплитуда которой постоянна по всей длине линии. Последнее обстоятельство обусловлено отсутствием затухания в линии.
График изменения амплитуды напряжения и тока в линии по ее длине для случая согласования представлен на рис. 3, а.
Холостой ход. В этом режиме ZН→ ∞, т.е. İН =0. Коэффициент отражения равен единице: ГН= 1. Таким образом, амплитуды обратной и прямой волн напряжения и тока равны, и в линии существуют так называемые стоячие волны напряжения и тока.
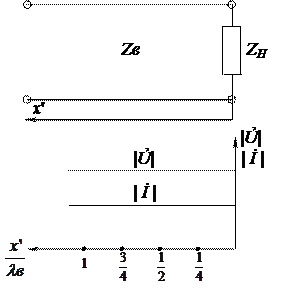 а) а) | 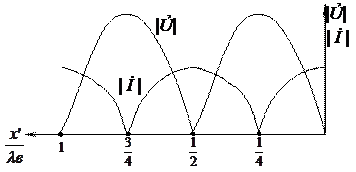 в) в) | ||||
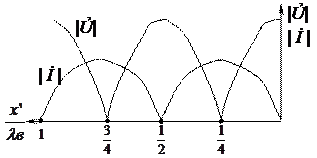 б) б) | 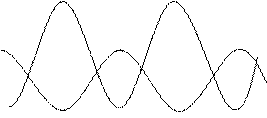
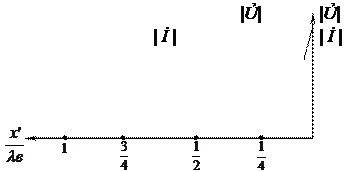 г) | ||||
| Рис. 1.3 |
Из (1.33) следует:
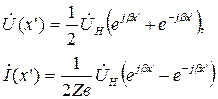
или
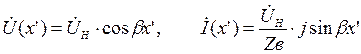 (1.35)
(1.35)
Заметим, что последние соотношения непосредственно следуют из (1.34) при İН =0.
Мгновенные значения:
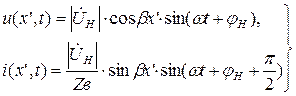 (1.36)
(1.36)
Выражение (1.36) представляют собой выражения для стоячих волн. Таким образом, в случае режима холостого хода распределение напряжения и тока в линии без потерь аналогично распределению типа «стоячая волна». Для такого режима характерно наличие в линии точек, в которых амплитуда колебаний равна нулю (узлы) и точек, в которых она максимальна (пучность). Определим координаты узлов и пучностей напряжений и токов.
В соответствии с (1.35) узлы напряжения находятся в точках, для которых сos 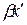 =0, и так как β=2π/λв, то координаты узлов напряжения:
=0, и так как β=2π/λв, то координаты узлов напряжения:
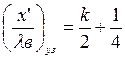 (1.37)
(1.37)
где k =0; 1; ….
Пучности напряжения находятся в точках, где cos 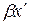 =±1. Откуда координаты пучностей напряжения:
=±1. Откуда координаты пучностей напряжения:
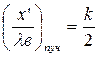 (1.38)
(1.38)
Аналогично для тока из (1.35) получаем
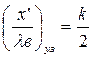 (1.39)
(1.39)
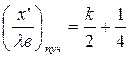 (1.40)
(1.40)
Как видно из (1.37)-(1.40), соседние узлы (пучности) как напряжения, так и тока находятся на расстоянии половины длины волны в линии один от другого, в то время как расстояние между ближайшими пучностями и узлами составляет четверть длины волны.
Отметим, что узлы (пучности) тока сдвинуты относительно узлов (пучностей) напряжения в режиме холостого хода на четверть волны. В нагрузке (k =0) находятся пучность напряжения и узел тока.
Распределение амплитуд тока и напряжения для режима холостого хода представлено на рис. 3, б.
Короткое замыкание. В этом случае ZН =0, т.е. ỦН =0. Из (1.25) следует, что ГН = 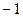 . Таким образом, амплитуды падающей и отраженной волн напряжения и тока равны, но сами эти волны сдвинуты по фазе на π.
. Таким образом, амплитуды падающей и отраженной волн напряжения и тока равны, но сами эти волны сдвинуты по фазе на π.
Как следует из (1.33),
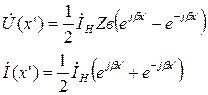
или
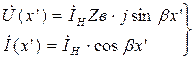 (1.41)
(1.41)
Как и в предыдущем случае, выражение (1.41) прямо следует из (1.34), если в (1.34) положить ỦН =0.
Мгновенные значения:
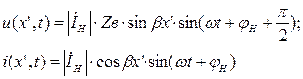 (1.42)
(1.42)
Последние выражения являются выражениями для стоячих волн. Таким образом, в случае короткого замыкания распределение напряжений и токов в линии без потерь аналогично распределению типа стоячих волн.
Аналогично предыдущему случаю координаты узлов и пучностей напряжения:
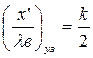 (1.43)
(1.43)
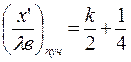 (1.44)
(1.44)
И координаты узлов и пучностей тока:
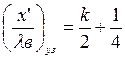 (1.45)
(1.45)
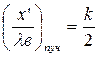 (1.46)
(1.46)
Характер распределения амплитуд тока и напряжения для режима короткого замыкания аналогичен случаю холостого хода. Отметим, что в данном случае в нагрузке (k =0) находится узел напряжения и пучность тока.
Распределение амплитуд представлено на рис. 3, в.
Общий случай. В предыдущих разделах были найдены распределения токов и напряжений в длинных линиях без потерь либо для случая полного отражения от конца линии (|ГН| =1), либо для случая отсутствия отражений (|ГН|= 0). В любом другом случае модуль коэффициента отражения меньше единицы и амплитуда отраженной волны меньше амплитуды падающей.
Положим в первом выражении (1.33) без потери общности 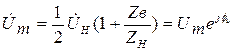 , а во втором выражении –
, а во втором выражении – 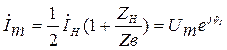 .
.
Тогда, учитывая, что ГН – комплексное число и, следовательно, 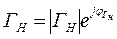 для уравнений (1.33) получим:
для уравнений (1.33) получим:
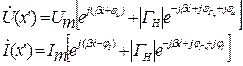 (1.47)
(1.47)
Для мгновенного значения напряжения в линии:
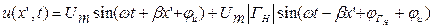 (1.48)
(1.48)
Добавим и вычтем в правой части (1.48) 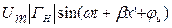 . После несложных преобразований получим:
. После несложных преобразований получим:
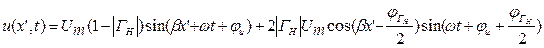 (1.49)
(1.49)
Аналогичное выражение получается и для тока 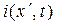
Как видно из (1.49), данный режим в линии без потерь можно рассматривать как наложение режимов бегущей волны (первое слагаемое) и стоячей волны (второе слагаемое) в (1.49). Подобный режим колебаний в линии называют режимом смешанных волн.
Определим распределение амплитуд напряжений и тока в длинных линиях без потерь в режиме смешанных волн.
Рассматривая первые слагаемые в (1.47), как комплексные амплитуды прямых волн, а вторые слагаемые – как комплексные амплитуды обратных волн, можно предположить, что максимальные значения амплитуды напряжения 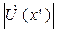 будут в тех точках линии, где прямые и обратные волны складываются в фазе, а минимальные значения этой функции – где падающие и отраженные волны складываются в противофазе.
будут в тех точках линии, где прямые и обратные волны складываются в фазе, а минимальные значения этой функции – где падающие и отраженные волны складываются в противофазе.
Таким образом, для максимальных значений 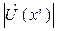 должно выполняться следующее соотношение:
должно выполняться следующее соотношение:
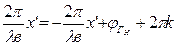 ,
,
а для минимальных значений:
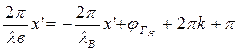
Тогда координаты точек максимальных и минимальных значений амплитуды напряжения 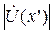 :
:
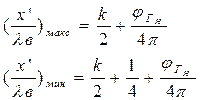 (1.50)
(1.50)
Из (1.47) и (1.50) следует, что в точках 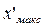 амплитуда напряжения равна
амплитуда напряжения равна
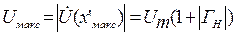 , (1.51)
, (1.51)
а в точках 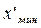 :
:
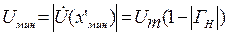 (1.52)
(1.52)
Что касается точек линий, в которых амплитуда тока достигает максимума и минимума, то в соответствии с (1.47) максимумы тока будут в тех точках, в которых падающая и отраженная волны тока складываются в противофазе, а минимумы тока будут в тех точках, где сложение этих волн – в фазе.
Тогда для координат максимумов и минимумов амплитуды тока получим:
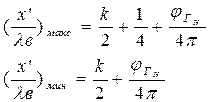 (1.53)
(1.53)
Из (1.47) и (1.53) следует, что
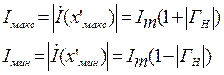 (1.54)
(1.54)
Значение амплитуд тока и напряжения в промежуточных точках можно найти из уравнений (1.47). Распределения 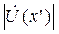 и
и 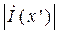 представлены на рис. 1.3, г (общий случай). Из рисунка видно, что максимумы и минимумы как напряжения, так и тока расположены с интервалом в половину длины волны, в то время как два соседних максимума и минимума сдвинуты на четверть длины волны.
представлены на рис. 1.3, г (общий случай). Из рисунка видно, что максимумы и минимумы как напряжения, так и тока расположены с интервалом в половину длины волны, в то время как два соседних максимума и минимума сдвинуты на четверть длины волны.
На практике часто используют величину, называемую коэффициентом стоячей волны (к.с.в.) – ρ:
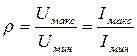 (1.55)
(1.55)
Учитывая (1.52) и (1.54), можно получить связь коэффициента стоячей волны с коэффициентом отражения:
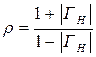 (1.56)
(1.56)
Очевидно, при согласовании 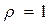 , во всех остальных случаях
, во всех остальных случаях 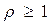 и стремится в бесконечность в режиме стоячих волн
и стремится в бесконечность в режиме стоячих волн 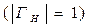 . Удобство практического использования величины ρ объясняется простотой его определения из экспериментально снятых распределений амплитуды тока и напряжения по длине линий. По известному ρ из (1.56) легко определяется модуль коэффициента отражения.
. Удобство практического использования величины ρ объясняется простотой его определения из экспериментально снятых распределений амплитуды тока и напряжения по длине линий. По известному ρ из (1.56) легко определяется модуль коэффициента отражения.
 2015-07-04
2015-07-04 2153
2153