Продолжение таблицы 10

XIX век	XX век	Средний вывод за XV— XX века
Деятельность Солнца	Эпидемия гриппа	Деятельность Солнца	Эпидемия гриппа	Пределы колебаний деятельности Солнца	Величина пределов	Пределы эпидемий гриппа	Величина пределов	Следование II волны через
макс	мин	макс	мин	макс.	мин.
		(98)– –02–03 –05–06 (II в.)				02-05	10-13		(98) 02-06 (II в.)
		15-16			–18–19	15-18	19-23		15-19
		27-28 29-32 (II в.)			26-27	26-29	33-34		26-30 (II в.)
		36-37				37-39	43- 45		36-38 42—44
		46-48 50-51 (II в.) 55 (III в.)				46-50	S5-56	4-5	(43) 46-51 (II в.)
		57-58 (II в.)				60-61	66-67		55-58 60-62 (II в.)
		73-75				69-82 (75)	75-79	3-6	67-76
		—				78-85	84-89		79-82
		89-91				88-94	98-001		88-93
								4,1 года*		4,3 года*

Примечание: Буква «В» обозначает волну.

* Величина пределов в среднем.

только влияние солнечного периода обусловливает появление эпидемий[52]. Солнечное влияние проявляется только в среднем, следовательно, и эпидемии могут различно располагаться по кривой солнцедеятельности, смотря по силе всех причин, но преимущественно появляясь именно за 2—3 года до или после максимума, подчиняясь фактору, еще нам не известному.

Затем, чтобы графически представить взаимоотношение между ходом гриппозных эпидемий, с одной стороны, и солнечными максимумами и минимумами — с другой, были построены кривые по тому же способу, что и при изучении движения холеры в России, т. е. при помощи наложения периодов по оси солнечных максимумов. Кроме того, гриппозные эпидемии были расположены и по оси солнечных минимумов (рис. 36).

При построении кривой А на оси ординат откладывались годы максимума солнцедеятельности. Влево от нее откладывались все эпидемии, находящиеся между минимумом — максимумом, а вправо — все эпидемии, находящиеся между максимумом — минимумом. По данному методу были построены кривые отдельно и общая кривая за XV — XX вв. Все они дают три подъема, из которых средний, совпадающий с осью максимума, оказывается наивысшим. Эпохи минимумов сопровождаются самым низким ходом кривой. Боковые подъемы приходятся на эпохи минимум — максимум, максимум — минимум. Наивысший подъем кривой по оси максимума объясняется из самой методики построения кривой: на эпохи максимума налагаются эпидемии, получившие начало в предыдущую эпоху минимума — максимума.

Для построения кривой A ₁ на оси ординат откладывались годы минимума солнцедеятельности. Влево от нее откладывались все эпидемии, имевшие место между максимумом и минимумом за весь указанный период по очереди. Вправо от нее — все эпидемии, имевшие место между минимумом и максимумом. Из рассмотрения полученной кривой явствует, что на три года минимального напряжения в солнцедеятельности падает за все столетия наименьшее количество гриппозных эпидемий. То же явление отчасти наблюдается и в эпоху максимума солнцедеятельности. Это явление хорошо объясняется самою методикой построения кривых. Наибольшее количество гриппозных эпидемий приходится между минимумом — максимумом, а чаще между максимумом — минимумом солнечной активности. Все выведенные ранее положения с тем же успехом могут быть получены при анализе данных кривых. Ввиду того что длительность солнечных периодов различна в обе стороны от осей максимума и минимума, для большей наглядности хода кривых А и А₁ пришлось сузить ее с боков до 11-летнего цикла (кривая В и B₁). Общие выводы здесь получили еще более наглядное выражение. Складывая вдвое эти смещенные кривые В и В₁, по осям минимума и максимума, мы получили кривые С и С₁, из которых чрезвычайно наглядно вытекает тенденция гриппозных эпидемий располагаться между минимумом — максимумом и максимумом — минимумом.

Затем, исходя из принятой нами методики, оказалось нетрудно установить промежуток времени между двумя волнами одной и той же эпидемической группы. Таковой промежуток оказался равным в среднем трем годам. Идеальное схематическое распределение эпидемий гриппа на солнечной кривой в случае одной или двух волн представлено на рис. 37.

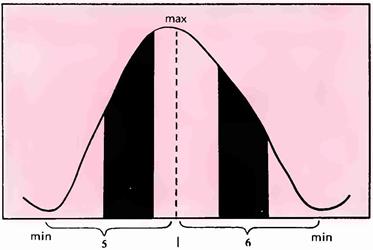
Рисунок 37. Схема идеального расположения эпидемий гриппа (в две волны)

Наконец, длительность одной эпидемии гриппа в одном периоде в среднем арифметическом за все столетия оказалась равной около двух лет. Для того чтобы еще более прочно установить зависимость эпидемий гриппа от состояния и деятельности Солнца, надо было прибегнуть к нижеследующему рассуждению.

Как известно, периоды пятнообразования распределены во времени более или менее закономерно: каждый период имеет в среднем арифметическом 11,1 года, и в столетие приходится по девять таковых периодов. Благодаря этим обстоятельствам точки максимальных напряжений в солнцедеятельности за время телескопических наблюдений за Солнцем колеблются в ограниченных пределах. Так, например, I максимум падает между 2 и 5 гг. каждого столетия, II — между 15 — 18 гг., III — между 26—30гг., IV — между 37—39 гг., V — между (46) 47—50 (51) гг., VI _ между 69—72 (75) гг., VIII — между 78—85 гг. и IX — между 88—94 гг. Сумма этих периодов максимальных лет солнцедеятельности равна 37 на столетие (37:100).

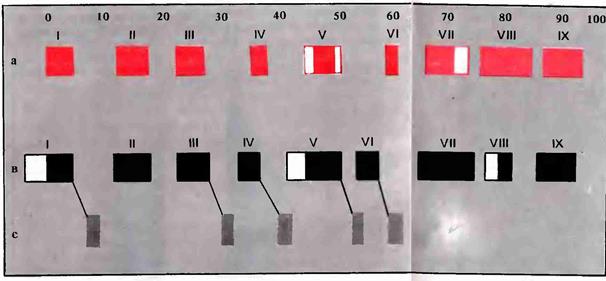
Рисунок 38. Соотношение между периодической деятельностью Солнца и эпидемиями гриппа за время с XV по XX в.
а — пределы колебаний солнечных максимумов за время с XV по XX в.;
b — пределы колебаний гриппозных эпидемий за то же время; с — вторичные волны эпидемий

Теперь обратимся к рассмотрению тех пределов, в которых колеблются за тот же промежуток времени гриппозные эпидемии. Оказывается, что пределы их колебаний как в среднем, так и для каждого отдельного случая лишь немного больше, чем пределы колебания солнечных максимумов. Так, например, колебания гриппозных эпидемий за тот же период времени ограничены следующими пределами (вторые волны эпидемий взяты в скобки): I. 2—6(9); II. 15—19; III. 26—30 (33); IV. 36—38 (42 — 43); V 47—51 (55); VI. 55—58 (60— 62);VII 67—76; VIII. 81—82 и IX. 88—93. Сумма этих лет равна 39 (без вторых волн) на столетие (39:100).

Сравнивая распределение во времени пределов колебаний дат максимумов с пределами колебаний гриппозных эпидемий, легко прийти к заключению, что пределы эти налагаются один на другой, оставляя между собою большие пустые промежутки, падающие на минимумы солнцедеятельности, и еще лишний раз подтверждая причинную зависимость одного явления от другого.

Окончательные положения и выводы представлены в таблице и графически изображены на рис. 38.

Обращаясь к табл. 10, мы встречаем весьма любопытное обстоятельство, а именно: сложив числа лет, занятых пределами колебаний максимумов солнцедеятельности за каждый век, за периоды XV — XIX вв., а затем те же данные за то же время для эпидемий гриппа и разделив полученные суммы на число периодов в столетие, будем иметь для солнцедеятельности 4,1, а для гриппа — 4,3. Это значит, что в среднем пределы колебаний солнечных максимумов и гриппа равны один другому. Разница, равная 0,2 года, должна быть объяснена неполнотою наших сведений как о гриппозных эпидемиях, так отчасти, только в меньшей степени, и о деятельности Солнца. Остановимся еще на одном замечании. Рассматривая распределение числа гриппозных заболеваний по СССР с 1923 по 1929 г., согласно Статистическому отделению Народного комиссариата здравоохранения, легко увидеть, что начиная с 1923 года — года минимума солнце-деятельности — по мере возрастания активности Солнца увеличивалось и число заболеваний гриппом (табл. 11, рис. 39).

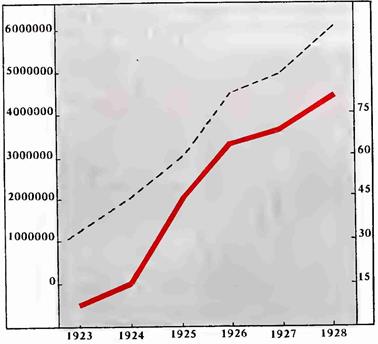
Рисунок 39. Верхняя кривая — заболеваемость гриппом в СССР с 1923 па 1928 г (годичные данные) Нижняя кривая — деятельность Солнца за то же время (годичные данные)

Обращает на себя внимание замечательный параллелизм двух наших кривых. Изломы кривой гриппа, означающей некоторую задержку в прогрессивном ходе эпидемий в точках 1926 и 1928 гг., чрезвычайно точно соответствуют аналогичной задержке роста солнечной активности за тот же период.

Таблица 11. Распределение заболеваемости гриппом по СССР (по четвертям -кварталам года)

	Годы
I II III IV	261 175 170 180 173 509 503 946	475 780 364 282 376 670 637 659	1 035 317 557 344 505 988 721 977	1 790 473 1 271 511 638 733 916 414	1 767 920 1 295 878 733 730 1 068 207	2 334 295 1 462 158 907 483 1 428 707	3 481 416 1 107 280 — —
	1 108 810	1 854 391	2 820 616	4 617 131	4 870 735	6 132 645	—

Таблица 12. Средняя месячная заболеваемость гриппом (по четвертям — кварталам года)

	Годы
I II III IV	87 058 56 727 57 836 167 982	158 593 121 427 125 556 212 553	345 106 189 115 163 663 240 659	596 824 423 837 212 911 305 471	589 306 431 959 246 243 356 069	778 098 487 386 302 494 476 235	1 160 472 369 093 — —

Таблица 13. Средние числа Вольфа — Вольфера (по четвертям — кварталам года)

	Годы
I	3,1	2,5	15,6	68,0	80,2	80,8
II	6,1	18,7	30,6	58,7	77,6	83,0	—
III	5,7	24,2	35,5	58,5	58,5	90,5	—
IV	8,1	21,5	75,4	70,5	54,6	53,6	—

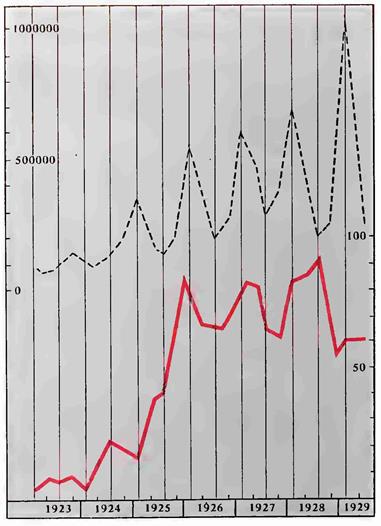
Рисунок 40. Верхняя кривая — заболеваемость гриппом в СССР с 1923 по 1928 г. (по четвертям года). Нижняя кривая — деятельность Солнца за тот же период (по четвертям года)

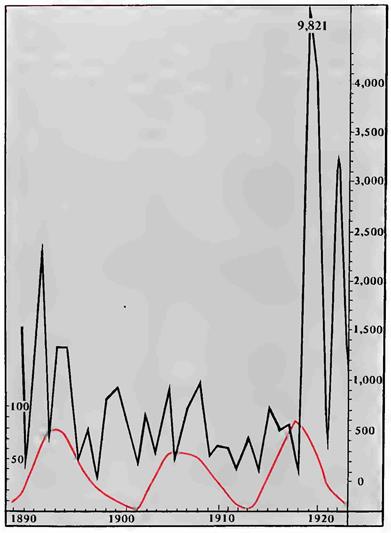
Рисунок 41. Верхняя кривая — грипп в Швеции с 1890 по 1923 г. (по Мигге}. Нижняя кривая — деятельность Солнца за тот же период

Но если мы рассмотрим движение тех же двух явлений по четвертям года (кварталам), то картина соответствия окажется еще более поразительной (табл. 12, 13, рис. 40). Изменения одной кривой сопровождаются изменениями другой: скачки гриппозной эпидемии либо точно совпадают с подъемами солнечной кривой, либо отстают на один-два сезона в зависимости от самого сезона года.

Материал, которым располагаем мы, еще не достаточен для окончательного вывода закона распределения гриппозных заболеваний во времени в связи с периодичностью Солнца. Но явления соответствия в ходе двух процессов сохраняют столь длительное постоянство, что принуждают к дальнейшему изучению намеченной здесь проблемы.

Наконец, нельзя не привести любопытные данные о соотношении между заболеваниями гриппа и солнечной деятельностью, которые мы находим у И. Мигге (Mygge; Копенгаген, 1930). Из приводимых на рис. 41 кривых видно, что максимальные скачки гриппозных эпидемий в Копенгагене с 1889 по 1922 г. падают на максимумы в деятельности Солнца, как, например, на годы 1892—1894, 1907 и 1918—1919.

Разделив весь имеющийся цифровой материал о гриппе в Копенгагене по семестрам, Мигге сопоставил его как с данными о солнцедеятельности, так и с частотой северных сияний. Он приводит интересное сопоставление, что явления солнечной деятельности, частота полярных сияний и частота случаев инфлуэнцы хорошо следуют одно за другим. Эта корреляция представляется тем более убедительной, что цифровые данные отнесены исключительно к Копенгагену, т. е. к району, ограниченному территориально. Значит, влияние солнечной активности может быть обнаружено и на материалах отдельных географических пунктов и районов.

Не лишены интереса приводимые нами диаграммы. Из них одна иллюстрирует распространение гриппа во французской армии по данным Делатера (Delater) и одновременный ход напряженности в деятельности Солнца (рис. 42), другие — грипп в Соединенных Штатах (рис. 43).

Говоря о соотношении между гриппом и активностью Солнца, следует упомянуть, что еще Буцорини (Buzorini) в 1830—1840 гг. пытался установить связь между вариациями электрического потенциала воздуха и эпидемиями инфлуэнцы. В последние годы прошлого столетия тот же вопрос изучался Мигге в Копенгагене, который, пользуясь электроизмерительными приборами

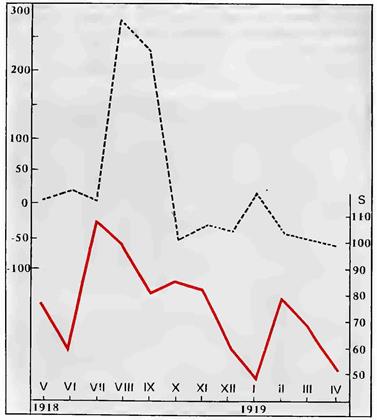
Рисунок 42. Верхняя кривая распространение гриппа so французской армии в 1918—1919 гг (по Далатеру). Нижняя кривая деятельность Солнца за тот же период

(капиллярный электрометр Оствальда), установил связь между колебаниями в атмосферном электричестве и вариациями эпидемии инфлуэнцы. Наблюдения Мигге, впрочем, нельзя признать достаточно убедительными. Как мы видели выше, работы Мигге по изучению влияния солнечных пятен на гриппозные эпидемии увенчались несколько большим успехом, чем его же работы по изучению влияния атмосферного электричества на ту же эпидемию.

Таким образом, изучая распределение эпидемий гриппа во времени, необходимо прийти к заключению, что распределение это не произвольно, а, наоборот, обнаруживает известную закономерность, степень которой увеличивается по мере привлечения к исследованию большего количества материала. Закономерность в распределении гриппозных эпидемий во времени, несомненно, стоит в некоторого рода

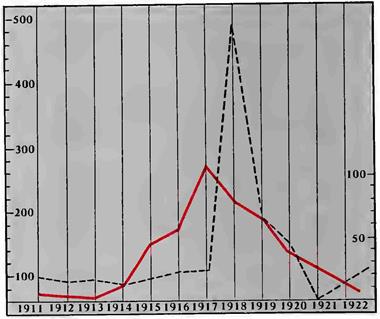
Рисунок 43. Кривая (пунктир) смертности от гриппа в США (по данным «Scientific American», november 1926) и деятельность Солнца (красная линия) с 1911 по 1922 г.

причинной связи с известными колебаниями в солнцедеятельности. Анализ явления позволяет определить, какие моменты в периодической деятельности Солнца наиболее благоприятствуют возникновению и развитию гриппозных эпидемий и какие моменты им не благоприятствуют. В то время как в годы минимального напряжения в деятельности Солнца мы встречаем небольшие и пространственно изолированные эпидемии, за незначительным исключением, в годы резких подъемов солнцедеятельности гриппозные пандемии стихийно схватывают огромные территории и уносят наибольшее число жертв.

Попытки определить периодичность в ходе гриппозных эпидемий и тем самым обусловить возможность прогноза были сделаны несколько лет назад в работах Ж. Броунли (Brownlee) и К. Сталибрасса (С. Stallybrass).

Статистические работы Броунли, произведенные с помощью метода периодограммы, установили для гриппозных эпидемий 1889—1891 гг., что максимум заболеваний приходится через каждые 33 недели. На основании, этого вывода Броунли осенью 1919 г. предсказал вспышку эпидемии гриппа в январе 1920 г.

Интересно отметить, что Э. Френкель обнаружила в деятельности Солнца такой же период, стоящий, как полагают некоторые астрономы, в связи с периодом сидерического обращения Венеры (224,7 дня).

Сталибрасс отмечает, что в распределении эпидемий гриппа в Англии за последние 130 лет можно обнаружить 10-летний период: 1789 — 1790; 1802—1803; 1830— 1832; 1840—1841; 1848—1849; 1854; 1869—1870; 1879; 1890—1891; 1898; 1918, а теперь, добавляю от себя, и 1927 г. Действительно, указанные Сталибрассом даты либо точно падают на эпохи максимума, либо на эпохи их назревания и падения.

Наконец, Б. Спир (В. Spear) разделяет год на 13 четырехнедельных периодов (28 дней). Было бы очень интересно проследить сопоставление хода гриппозных эпидемий (а также и других эпидемических заболеваний) с изменениями в ходе атмосферного электричества по тропическому месяцу (27,32 дня), стоящего в связи с положением Луны и влиянием Солнца. Еще Св. Аррениус разработал статистику заболеваний бронхитом и общую статистику смертности в течение тропического месяца. Тот же ученый, пользуясь методом гармонического анализа, показал на большом статистическом материале очевидную корреляцию между ходом атмосферного электричества как по тропическому месяцу в 27,32 дня, так и по 25,929-дневному периоду и рядом физиологических отправлений и нервно-психических явлений.

Максимум физиологического воздействия для всех исследованных явлений приходится спустя один день после максимума атмосферного электричества.

Наконец, еще следует указать следующее: эпидемиологами замечено, что время от времени гриппозные эпидемии принимают чрезвычайно жестокие формы и что такого рода эпидемии повторяются каждые 35 лет. Между тем Честер при помощи гармонического анализа нашел в деятельности Солнца период, весьма близкий к 35 годам, а именно 33,375 года, которые обусловливают усиление в солнцедеятельности каждые 33,375 года.

Обнаружение некоторых любопытных соотношений между ходом солнцедеятельности и эпидемиями гриппа принуждает к более детальному исследованию явления при помощи применения математического анализа к точной статистике гриппозных заболеваний, что и ставит своею ближайшей задачей автор данной работы.

Резюмируя вышеизложенное о распределении гриппозных эпидемий во времени в связи с периодическою деятельностью Солнца, мы можем сказать следующее:

1. Период гриппозных эпидемий в среднем арифметическом равен 11,3 года.

2. Отклонение начальных лет эпидемий от максимума солнцедеятельности в ту или другую сторону равно в среднем 2,3 года. Иными словами, эпидемии гриппа имеют тенденцию начинаться за 2,3 года до максимума или спустя 2,3 года после такового.

3. Длительность эпидемии (повсеместно) в каждом 11-летнем солнечном периоде в среднем равна четырем годам.

4. Если эпидемия дает вторую волну в том же солнечном периоде, последняя отстоит от окончания первой эпидемической волны в среднем на три года.

5. Таким образом, после года минимума в солнце-деятельности, приблизительно через три года, всегда можно ждать первой волны эпидемии.

6. Вторые и третьи волны эпидемии уже налагаются на годы после максимума, т. е. находятся на уклоне в пятнообразовательном процессе.

7. Интенсивность эпидемии, по-видимому, находится в известной зависимости от интенсивности в деятельности Солнца.

8. Сезонный фактор играет ту роль, что приближает или отдаляет вспышку эпидемии.

9. На основании изложенного открывается возможность сделать прогноз о наиболее вероятном размещении во времени эпидемий гриппа на некоторый срок вперед[53].

Нами было обращено внимание на то обстоятельство, что наиболее сильные и смертоносные эпидемии возвратного тифа в XIX в. падают на годы максимального напряжения в солнцедеятельности. Ввиду того что симптомокомплекс возвратного тифа был окончательно выделен лишь в прошлом веке и получил подтверждение в открытии О. Обермейером (О. Obermeier) особых микроорганизмов — спирохет возвратного тифа, вопрос о распределении эпидемий возвратного тифа за прошлые века остается открытым: еще в середине прошлого века дифференциальная диагностика тифозных заболеваний была чрезвычайно слабой.

Поэтому наш исторический обзор приходится начинать с 1816 г., когда возвратный тиф с большой силой вспыхнул в Великобритании и Ирландии.

Как раз в 1816 г. имел место максимум активности Солнца, когда показатель этой активности — относительное число Вольфа — Вольфера S = 45,83[54].

В конце этого года эпидемия возвратного тифа вспыхнула в Ирландии, где и свирепствовала в течение 1817 и 1818 гг. Многие английские врачи причисляют эпидемию 1816—1819 гг. к возвратной горячке («relapsing fewer»), считая ее родственной с сыпным тифом.

Следующее появление возвратного тифа в Европе произошло через 10—11 лет, в 1826 г., в Ирландии. В 1827—1828 гг. возвратный тиф резко усилился, и, согласно мнению Мёрчисона (Murchison), в это время впервые симптомокомплекс возвратного тифа был выделен с достаточной ясностью. Также и данное появление возвратного тифа произошло в годы максимальной напряженности в деятельности Солнца, когда годовое относительное число пятен колебалось в пределах 50—70. Максимум солнцедеятельности отнесен к 1829—1830гг.

Временем следующего появления возвратного тифа обычно считают 1843 г., когда возвратный тиф наблюдался в Англии. Это был год минимума солнцедеятельности, когда S = 10,7. И действительно, тифозная эпидемия протекала в ограниченных размерах и смертность от нее была невысока. Здесь можно заметить, что еще за два года до 1843 г., а именно в 1841—1842 гг., когда деятельность Солнца находилась в пределах S = 37—25, в некоторых местах Европы имели место эпидемические вспышки возвратного тифа.

Затем в 1848 г., в год максимума солнцедеятельности, когда S = 124,3, снова имела место в Ирландии эпидемия возвратного тифа с большим процентом смертности. В то же время возвратный тиф появился в Англии, откуда проник во Францию («fievre de rechute»). Постепенно уменьшаясь, возвратный тиф в Англии держался до года минимума солнцедеятельности — 1856, когда S = 4,3, после чего совершенно исчез из Англии.

Следующая вспышка возвратного тифа произошла в Одессе в 1863 г. и в Петербурге в 1864 г., что хорошо совпадает с достаточно сильной деятельностью Солнца, хотя и находящейся уже на склоне: в 1863 г. S = 44,0, в 1864 г. S = 47,0. В Петербурге эпидемия возвратного тифа, постепенно ослабевая, держалась вплоть до года минимума солнцедеятельности — 1867 г., когда S = 7,3.

Наконец, следующее пандемическое распространение по Европе возвратного тифа как раз падает на годы резко повышенной (сравнительно со всеми предыдущими периодами) деятельности Солнца, а именно на 1868— 1872 гг. Вот астрономические данные относительно чисел Вольфа — Вольфера:

Таблица 14.

1868 г.. S=37,3 1869 г. S=73,9 1870 г. S=139,1 1871 г. S=111,2 1872 г. S=101,7

В эти годы наблюдалось не только быстрое распространение эпидемии, но и высокая смертность от нее.

Начиная с этой эпохи возвратный тиф в большинстве европейских стран резко пошел на убыль, по-видимому, благодаря культурному фактору. Однако он остался в России и эндемически проявлял себя. Поэтому представлялось любопытным выяснить вопрос, насколько возвратный тиф в пределах России следует отмеченной закономерности. И это тем более казалось интересным, что я не нашел в имевшихся в Москве иностранных источниках статистических данных о возвратном тифе за более или менее длительные периоды времени.

Наиболее полной статистикой заболеваемости возвратным тифом можно считать таковую по Европейской России, где она ведется начиная с 1883 г., т. е. как раз со времени последующего за 1870 г. периода максимального напряжения в солнцедеятельности. Уже из беглого просмотра статистического материала легко было заметить последовательную чередуемость числовых величин. Эта чередуемость обнаруживает периодичность, хорошо совпадающую с периодичностью солнцедеятельности.

Таблица 15. Периодичность в солнцедеятельности и заболеваемости возвратным тифом

№	Периоды солнцедеятельности:максимумы (1-8), минимумы (1)	Среднее число W — W за данный 3—летний период солнцедеятельности	Периоды эпидемии возвратного тифа	Среднее число W — W в период эпидемии	Приблизительная оценка смертности
1 макс.	1815-1817	40,7	1816-1818	39,1	Значительная
2 макс.	1823-1830	66,8	1827-1828	56.1	Высокая
1 миним.	1842-1844	16,6	1842-1843	17,4	Средняя
3 макс	1847-1849	106,2	1848-1849	110,1	Значительная
4 макс.	1859-1861	88,9	1863-1864	45,5	Значительная
5 макс.	1869-1871	108,0	1869-1872	106,7	Высокая
6 макс	1882-1884	62,3	1883-1885	59,8	Средняя
7 макс.	1905-1907	59,7	1906-1909	54,7	Значительная
8 макс	1916-1918	80,5	1919-1920	50,6	Значительная

Так, в годы максимума солнцедеятельности — 1883 — 1885, когда S = 63—52, мы имеем наиболее высокие цифры заболеваемости, которые постепенно уменьшаются к периоду минимума солнцедеятельности. Тот же материал говорит о повышениях заболеваемости возвратным тифом в России в периоды 1906—1909 гг.— в эпоху максимальной деятельности Солнца (1905—1907 гг.) и в последующую эпоху максимума (1917—1918 гг.). Промежуточные эпохи минимумов солнцедеятельности (1900—1902 и 1913 гг.) дают минимум заболеваний.

Собранные данные представлены в табл. 15.

Необходимо заметить, что статистика возвратного тифа с 1883 г. по всей России не отличается все-таки необходимой точностью и однообразностью: в истекшем столетии ряд губерний не имел еще медицинской статистики, в других губерниях она собиралась недостаточно бережливо или с большими промежутками. Учесть и выделить все данные факторы по всей Европейской России с 1883 г. не представляется возможным. Мы приведем лишь диаграмму заболеваемости с 1899 по 1925 г. За этот срок цифры достоверны (рис. 44).

Поэтому для дальнейшей обработки была принята статистика заболеваемости возвратным тифом по городу Москве с 1883 по 1918 г. как наиболее точная из всех существующих. После нанесения цифровых данных на систему координат представилась возможность сличения полученной кривой с синхроничною ей кривою солнцедеятельности. Тут впервые была обнаружена замечательная закономерность в ходе этих двух кривых (рис. 45).

Так, подъемам одной соответствуют во времени подъемы другой; их падения также происходят синхронно. Сей параллелизм в ходе кривых говорит об известной связи между ними. В целях установления тесноты этой связи и ее количественной оценки было решено прибегнуть к одному из методов математической статистики — методу корреляции.

Дабы элиминировать выступы и зигзаги наших рядов и тем устранить мелкие и случайные колебания, было произведено сглаживание рядов по трем точкам по формуле невзвешенной скользящей средней:

a_i-1+a_i+a_i+1

b_i =,

где b_i — член сглаженного ряда, a_i — член эмпирического ряда. В результате были получены сглаженные ряды, состоящие из скользящих средних (табл. 16 и 17).

Как известно, для предотвращения искажения коэффициента корреляции необходимо исключить уровни наших эмпирических рядов и затем уже исследовать корреляцию отклонений от уровня.

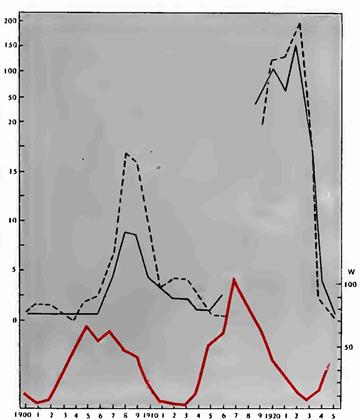
Рисунок 44. Заболеваемость возвратным тифом в России и СССР с IS99 по 1925 г. (сплошная кривая) и на Украине {пунктир) на 10 000 населения (по Добрейцеру). Нижняя кривая — деятельность Солнца

Уровень солнцедеятельности легко определить из непосредственного рассмотрения графика; уровень, очевидно, будет параллелен оси абсцисс, поскольку он не заключает в себе уровня динамического ряда, колеблясь около постоянной величины (37,9), т. е.средней арифметического ряда.

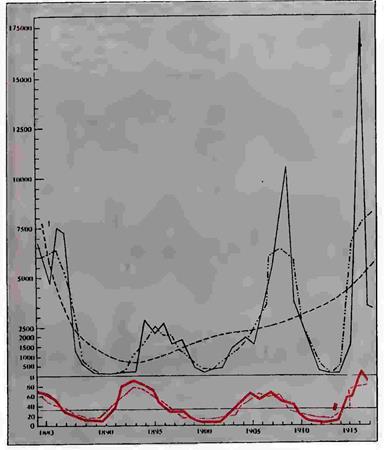
Рисунок 45. Верхние кривые — заболеваемость возвратным тифом в Москве с 1883 по 1918 г.:
————————эмпирический ряд,
—.—.— сглаженный ряд по трем точкам.
— — — — — — выровненный по параболе 4-го порядка,
Нижние кривые — пятнообразовательная деятельность Солнца,
————————эмпирический ряд,
.—.—.— сглаженный ряд

Так как уровень возвратного тифа непосредственно из диаграммы не определяется, пришлось прибегнуть к аналитическому выравниванию.

Выравнивание эмпирического ряда возвратного тифа было произведено нами по параболе четвертого порядка. В качестве критерия пригодности данной параболы служат обычно суммы квадратов разностей между значениями эмпирического и выравненного ряда, причем это проверяется также и кумуляцией (последовательным суммированием) отклонений от уровня. Весьма прихотливый рисунок рядов возвратного тифа не позволяет воспользоваться для уровня параболами низших степеней, как, например, параболой 1-го или 2-го порядка. Здесь необходима большая степень свободы аналитической кривой, которая могла бы выделить из ряда те долговременные колебания в движении эпидемии, которые отнюдь не связаны с ходом солнечных процессов, а определяются иными причинами. Характер ряда — резкие подъемы в начале и конце, а также некоторое усиление к середине — вынуждает пользоваться именно параболой 4-го порядка, которая в состоянии следовать столь сложным изгибам.

Как показывает опыт, во многих случаях, когда необходимо отделить закономерное движение явления, представляемого статистическим рядом, от его хаотических колебаний, благодаря действию случайных причин, так называемое параболическое интерполирование (т. е. выравнивание статистического ряда посредством параболических кривых) дает хороший результат. Мы воспользовались способом, изложенным В. Хотимским, поскольку он, в отличие от традиционного способа «нормальных уравнений» дает значительное сокращение вычислительной работы и имеет целый ряд других весьма важных преимуществ. Общий вид параболы, в соответствии с которой, как мы полагаем, происходит изменение уровня статистического ряда таков:

f(X) = а₀ + а₁Х + а₂Х² + а₃Х³ +... a_mX^m

Параболическое выравнивание сводится по существу к определению параметров параболы а₀, a_1, а₂,...а_т.

Таблица 16

№	Год	Солнечные пятна	Сглажен по трем точкам	Отклонения x— X	Отклонения, сглаженные по трем точкам
		63,7	—	+ 25,8	—
		63,5	60,0	+ 25,6	+ 21,9
		52,2	47,0	+ 14,3	+ 9,1
		25,4	30,2	-12,5	- 7,7
		13,1	15,1	-24,8	-22,8
		6,8	8,7	-31,1	-29,2
		6,3	6,7	-31,6	-31,2
		7,1	16,3	-30,8	-21,6
		35,6	38,6	- 2,3	+ 0,7
		73,0	64,5	+ 35,1	+ 26,6
		84,9	78,6	+ 47,0	+ 40,7
		78,0	75,6	+ 40,1	+ 37,7
		64,0	61,3	+ 26,1	+ 23,4
		41,8	44,0	+ 3,9	+ 6,1
		26,2	31,6	-11,7	- 6,3
		26,7	21,7	-11,2	-16,2
		12,1	16,1	-25,8	-21,8
		9,5	8,1	-28,4	-29,8
		2,7	5,7	-35,2	-32,2
		5,0	10,7	-32,9	-27,2
		24,4	23,8	-13,5	-14,1
		42,0	43,3	+ 4,1	+ 5,4
		63,5	53,1	+ 25,6	+ 15,2
		53,8	59,8	+ 15,9	+ 21,9
		62,0	54,8	+ 24,1	+ 16,9
		48,5	51,5	+ 10,6	+ 13,6
		43,9	37,0	+ 6,0	- 0,9
		18,6	22,7	-19,3	-15,2
		5,7	9,3	-32,2	-28,6
		3,6	7,8	-34,3	-34,3
		1,4	4,9	-36,5	-33,0
		9,6	19,5	-28,3	-18,4
		47,4	38,0	+ 9,5	+ 0,1
		57,1	69,5	+ 19,2	+ 31,6
		103,9	80,5	+ 66,0	+ 42,6
		80,6	—	+ 42,7	—

Σ x_i =1363,6 Σ x_i =—77,0

X=37,9 (Σ x_i)²=5929,0

Таблица 17

№	Год	Возврати. тиф y	Сглажен. у по трем точкам	Теорет. у (парабола 4-го порядка)	у-v отклонение в %	Отклонение сглажено по трем точкам
			_	7 684,63	- 19	_
			6 201	5 996,10	- 23	+ 9,0
			6 581	4 601,81	+ 69	+ 52,7
			5 498	3 470,38	+ 112	- 147,7
			3 008	2 572,11	- 47	- 6,0
				1 878,98	- 83	- 743
				1 364,65	- 93	- 81,0
				1 004,46	- 97	- 95,3
				775,43	- 96	- 91,3
				656,26	- 81	- 85,0
				627,33	- 78	+ 53,3
				670,70	+ 312	+ 138,7
		2 116		770,11	+ 175	+ 229,3
				910,98	+ 194	+ 134,0
				080,41	+ 33	+ 88,3
			1 153	267,18	+ 38	- 3,3
				461,75	- 81	- 47,3
				656,26	- 99	- 89,3
				844,53	- 88	- 89,3
				2 022,06	- 81	- 68,7
				2 186,33	- 37	- 45,7
				2 335,30	- 19	- 34,0
				2470,41	- 46	- п,з
				2 593,58	+ 31	+ 26,7
				2 708,71	+ 95	+ 134,7
				2821,38	+ 278	+ 133,7
				2 938,85	4- 28	+ 97,7
				3 070,06	- 13	- 15,3
				3 225,63	- 61	- 56,7
				3417,86	- 96	- 84,7
				3660,73	- 97	- 973
				3 969,90	- 99	- 87,7
				4362,71	- 67	+ 34,3
				4858,18	+ 269	+ 57,3
				5 477,01	- 30	+ 66,0
				6241,58	- 41	~~

Σ y_i =98 575,00 Σ y_i =98 654,04 Σ y_i =+124,90

(Σ y_i)²=15 600,01

Для решения задачи вычисляем члены интерполяционного ряда П. Л. Чебышева, применяя таблицы, составленные В. Хотимским,—получаем уравнение параболы 4-го порядка, соответствующей статистической кривой возвратного тифа[55]:

Y = 9700,46 — 2190,92 X + 180,95 X² — 5,93 X ³ + 0,07 X⁴

Полагая X— 1, 2, 3,..., 36, получаем соответственные значения для Y и строим график параболы, где нулевая точка X = 0 отнесена к 1882 г. Следовательно, X = 1 соответствует 1883г. и т. д.

Затем производим вычисления отклонений от найденного уровня для корректирования наших рядов. Корректируем ряд возвратного тифа по формуле:

y_i – Y

* 100,

I

где у — член эмпирического ряда, Y — член теоретического ряда. В результате получаем выправленный ряд, графически представленный на рис. 46, табл. 17.

Эмпирический ряд чисел W—W корректируется по более простой формуле:

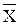x_i –

где х_i — член эмпирического ряда, 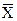— их средняя арифметическая. Выправленный ряд солнечных пятен представлен на рис. 47, табл. 16.

В первом случае избран более сложный способ, предложенный Пирсонсом (Pearsons), так как есть основания думать, что величина отклонений связана с высотой уровня.

Наконец, производим сглаживание выправленных рядов по трем точкам в целях элиминирования мелких случайных колебаний. Результаты сглаживания представлены на чертежах пунктирными линиями.

После этого приступаем к количественному определению тесноты связи между нашими рядами с помощью коэффициента корреляции.

Вычисление коэффициента корреляции производится, как известно, по формуле Пирсонса:

1/n* Σ x_iy_i

r ₌

σ_xσ_y

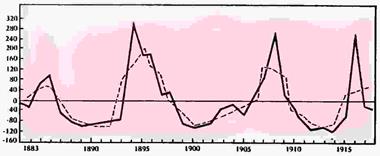
Рисунок 46. Возвратный тиф в Москве с 1883 по 1918 г Отклонения эмпирических значений у от теоретических значений Y в %
y_i-Y
*100
Y

— — — — та же кривая, сглаженная по трем точкам

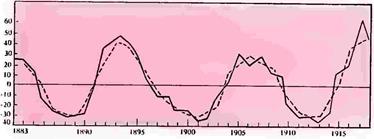
Рисунок 47. Пятнообразовательная деятельность Солнца с 1883 по 1918 г Отклонения эмпирических значений от среднего арифметического
—————— кривая х—X
— — — — та же кривая, но сглаженная по трем точкам

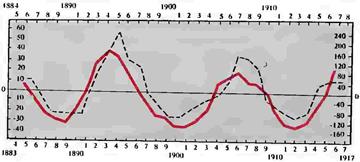
Рисунок 48. Сопоставление отклонений возвратного тифа, сдвинутых на один год влево (пунктир), с отклонениями данных о солнцедеятельности Коэффициент корреляции r = +0,88±0,03

Эта формула может быть представлена в таком виде:

n Σ (xy)- Σ x Σ y

r =

[n Σ x²-(Σ x)²][n Σ y²-(Σ y)²]

Пользуясь материалом, данным в таблицах, и подставляя в формулу соответствующие числовые величины наших отклонений, находим коэффициент корреляции.

Вероятную ошибку коэффициента корреляции вычисляем по формуле:

ε = 0,6745 1-r²

n

где r — коэффициент корреляции, п — число точек ряда, 0,6745 — константа нормальной кривой ошибок.

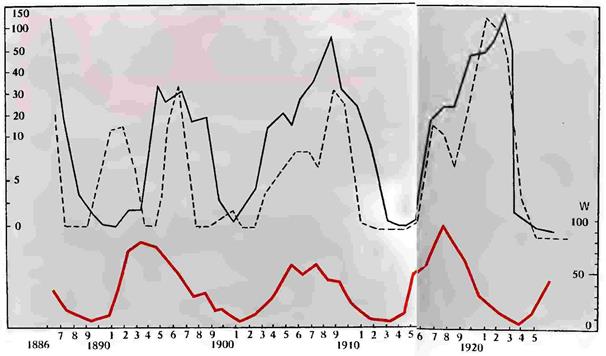
Рисунок 49. Заболеваемость возвратным тифом в Москве (сплошная линия) и Ленинграде (пунктир) с 1886 по 1925 г. на 10 000 населения (по Добрейцеру). Нижняя кривая — деятельность Солнца

Пользование этой формулой для вычисления вероятной ошибки в случае временного ряда, вообще говоря, не может быть признано вполне соответственным, однако при наличии достаточно высоких коэффициентов корреляции оно дает удовлетворительные результаты.

Результат вычислений можно резюмировать так.

Между ходом возвратного тифа в Москве и числами Вольфа — Вольфера (W — W) за время с 1883 по 1918 г. включительно коэффициент корреляции оказался равным:

1. При синхронном сопоставлении

r = +0,67 ± 0,06.

2. При левостороннем сдвиге кривой возвратного тифа на один год

r = +0,88 ± 0,03.

3. При левостороннем сдвиге кривой возвратного тифа а два года

r = +0,82 ± 0,04.

Следовательно, при левостороннем сдвиге на один год кривой возвратного тифа мы констатируем максимум тесноты связи по сравнению с другими положениями кривой. Это значит, что максимум заболеваний возвратным тифом следует год спустя после максимума солнцедеятельности. Полученный в данном случае коэффициент корреляции г = + 0,88 ± 0,03, как лежащий в пределах 0,7—0,9, согласно Чеддоку, указывает на высокую степень зависимости наших рядов.

Действительно, рассматривая наши кривые, представленные на рис. 48, легко прийти к заключению об исключительно тесном совпадении в ходе кривых отклонений возвратного тифа и чисел Вольфа — Вольфера. Это совпадение обнаруживается из года в год на протяжении 35 лет, за которые мы имеем 4 максимума и 3 минимума солнцедеятельности. Не указывает ли это на тесную причинную зависимость усилений и ослаблений возвратного тифа от соответственных колебаний в состоянии и составе окружающей нас физико-химической среды, зависящей от мощных периодических изменений в деятельности Солнца?

Приводимые здесь еще кривые (рис. 49 и 50) заболеваемости и смертности от возвратного тифа хорошо подтверждают все вышесказанное. Остается отметить лишь полную синхронность заболеваемости и смертности в Москве и Ленинграде. Факт синхроничности говорит за существование общей причины, обусловливающей колебания в изучаемых нами явлениях.

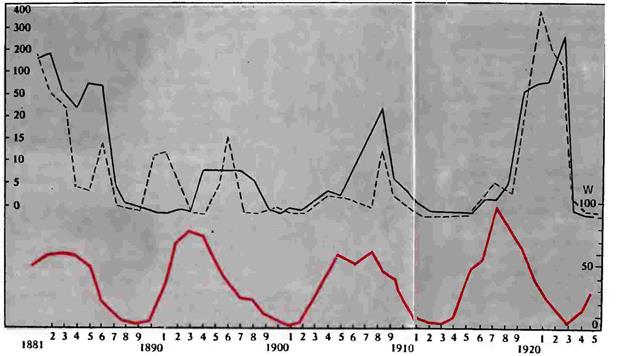
Рисунок 50. Смертность от возвратного тифа в Москве (сплошная линия) и Ленинграде (пунктир) с 1S81 по 1925 г. на 100 000 населения (по Добрейцеру).
Нижняя кривая — солнцедеятельность

Правда, нам могут быть сделаны следующие возражения: хотя подъемы и падения кривой возвратного тифа хорошо совпадают с соответствующими моментами в деятельности Солнца, некоторые из них также совпадают и с известными явлениями социальной и экономической жизни государства, как, например, с эпохами голода в 1892—1893 гг[56].

Но, как известно, возвратный тиф господствует главным образом среди плохой гигиенической обстановки, в грязных, переполненных народом помещениях, во времена социальных неурядиц и стихийных бедствий.

Конечно, было бы совершенно неосновательно отрицать влияние данных моментов на численность заболеваний: резкие уклонения от обычной нормы социально-экономических условий должны неминуемо усилить или даже вызвать ту или иную эпидемию. Это положение встречает поддержку на каждом шагу. Но в то же время было бы также неосновательно придавать указанным социально-экономическим явлениям исключительное значение как единственному актуальному фактору в этиологии эпидемии. История знает сильнейшие социальные потрясения, не сопровождавшиеся сколько-нибудь значительными по размеру повальными заболеваниями. И за такую умеренную точку зрения говорит ход кривых отклонений возвратного тифа, которые необычайно пластично следуют ходу чисел Вольфа — Вольфера, и не только в эпохи максимумов, но также и в эпохи минимумов и в годы, свободные от тех или иных общественных потрясений, что особенно знаменательно. Вместе с тем полной согласованности между численностью заболеваний и числами Вольфа — Вольфера в годы максимумов нет. Данное несоответствие на высоте скачков возвратного тифа зависит от социально-экономических факторов, колеблемости численности населения и других причин.

Но это не дает оснований для умаления роли влияний изменчивости внешних условий природы на силу эпидемии, для объяснения ее исключительно следствием воздействия на человека факторов социально-экономического порядка. Вероятнее всего, все социальные и природные факторы объединены в один комплекс, влияние которого и выражается в прихотливом ходе кривой.

Иначе как бы мы могли объяснить себе тот факт, что ряд других эпидемических заболеваний также имеет тенденцию так или иначе изменяться в годы максимумов солнцедеятельности, давая 11-летнюю периодичность совершенно независимо от местных и социально-экономических условий. В истории эпидемий и пандемий мы часто встречаем исключительные совпадения в развитии сильнейших эпидемий и эпох солнцедеятельности.

Обратимся к могущественной международной эпидемии — чуме и постараемся выяснить, имеется ли какая-нибудь зависимость между возникновением, интенсивностью и распространением ее и пятнообразовательной деятельностью Солнца.

Из глубокой древности до нас дошли сведения об этой страшной болезни. Опустошения, произведенные ею, описываются в древних летописях. Древнегреческие писатели и историки: Гомер, Платон, Геродот, Фукидид, Гиппократ, а также древнеримские писатели и историки: Ливии, Тацит и другие — упоминают о чумных эпидемиях.

Цезарь во второй книге о междоусобной войне говорит о чуме, свирепствовавшей в 49 г. до н. э. Поэты Виргилий и Овидий тоже описывают чуму. Кроме того, известны большие чумные эпидемии, носящие название чумы Орозия (125 г. н.э.), чумы Антонина и Галена (165 — 168 гг.), чумы Киприана (251—266 гг.) и чумы Юстиниана (531—580 гг.). Относительно всех этих древних эпидемий в литературе нет точных указаний о течении и симптомах болезни, но чума Юстиниана была действительно настоящей эпидемией бубонной чумы в современном смысле этого слова.

Гезер на основании достаточно веских исторических данных полагает, что родиной бубонной чумы следует считать Египет, где опустошительные эпидемии этой болезни, несомненно, имели место за 300 лет до нашего летоисчисления. В свидетельствах современника Трояна Руфа из Эфеса (I в. н.э.) имеется первое достоверное свидетельство о появлении бубонной чумы в Египте с достаточно подробным описанием симптомокомплекса болезни. Со времени VI столетия н.э. по XIII в. включительно все чаще и чаще встречаются упоминания об опустошительном действии чумных эпидемий, но исторические сведения об этих эпидемиях не могут быть признаны вполне точными.

С VII по XIV в. чума наблюдалась в Византии, Риме и других.местах Италии, в Галлии и Германии. А в IX в. большая чумная эпидемия произвела опустошение почти во всей Европе. В XI в. чума впервые появилась в Польше и России. В следующем веке она неоднократно посещала Европу, а в XIIIв. ею были опустошены Сирия, Греция, Италия и другие страны Европы, а также ряды крестоносных войск Балдуина. В XIV в. чума под названием черной смерти (mor nigra) достигает беспримерного в истории распространения и силы. Возникнув в Индокитае, в Средней Азии, пандемия черной смерти распространялась при посредстве торговых караванов, проникла на побережья Каспийского, Черного и Средиземного морей и уже отсюда в Европу, где унесла в короткий срок до четверти всего населения.

В XIV в. чумные эпидемии погубили 25 млн, человек (J. Hecker), но особенной частоты чума достигла в России в XV, XVI и XVII вв. В XV в. чума в Европе почти не прекращалась, постоянно ослабевая и усиливаясь, обнаруживая себя то на Западе, то главным образом на Востоке. Это же самое можно сказать и о XVI и XVII вв., и только в самом конце XVII в. Европа несколько отдохнула от ужасов чумы. Однако уже с начала XVIII в. возникает новая эпидемия чумы, за которой следуют другие. В XIX в. чума гнездится в Египте, Алжире, Персии и Армении, откуда периодически распространяется по Европе. Кроме того, она эпидемически проявляет себя в Индии, откуда распространяется в Азию и Африку.

Эпидемиология чумы не в состоянии объяснить то несомненное явление, что чумные эпидемии и пандемии возникают и распространяются в достаточной степени произвольно. Нет никаких положительных данных о влиянии на ход чумы хотя бы таких значительных явлений, как атмосферные осадки или уровень почвенных вод; правда, климат и температура, а также социальные и гигиенические условия жизни играют в распространении чумы далеко не последнюю роль.

Но всех этих данных для суждения о причинах возникновения и развития чумы еще очень недостаточно.

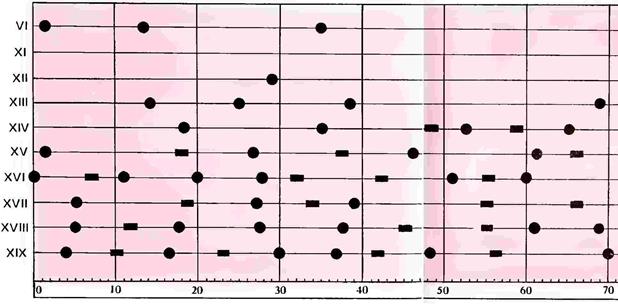
Рисунок 51. Диаграмма распределения чумных эпидемий во времени и связи с ходом периодической деятельности Солнца с VI по XX в. Черные кружки — даты эпидемий чумы. падающих на максимум солнце-деятельности.

Так, климат и температура, а равно и одинаковые социальные и санитарные условия встречаются ежегодно во многих местах земного шара, а чумные эпидемии далеко не всегда сопутствуют им.

«Причина болезни,— пишет Гезер о чуме,— покрыта глубоким мраком; температура, погода, климат остаются без всякого влияния если не на происхождение, то по -крайней мере на распространение болезни, которая господствовала во все времена года и на равнинах, и на горах высотой до 10 тыс. фут над уровнем моря».

Далее Гезер пишет: «Чума в Египте может развиваться самобытно; это уже в древности считалось несомненным фактом, но причины этого явления и теперь так же темны, как две тысячи лет тому назад».

Мало того, сплошь да рядом чума захватывает области с культурным населением, и, наоборот, присутствие всех условий, могущих вполне способствовать развитию чумной эпидемии, не вызывает чумы, хотя единичные случаи, завезенные извне, и констатируются бактериологами, а следовательно, есть и те микроорганизмы, которые могли бы, очевидно, в другое время вызвать вспышку этой болезни.

Изучение вопросов эпидемиологии чумы показало, что отсутствие даже продолжительное время заболеваний чумою среди людей в каком-либо месте еще не означает отсутствия чумного вируса в этом месте. Констатированы случаи чумы среди людей после 10-летнего промежутка, причем чумной вирус хранился и размножался в организме крысы.

Следовательно, остается совершенно невыясненным вопрос о том, какие именно факторы модифицируют патогенную способность чумного вируса и тем самым кладут начало чумным эпидемиям или, наоборот, прекращают их победоносное шествие. Этот вопрос — одна из загадок современной эпидемиологии.

Не углубляясь здесь в рассмотрение достаточно большого количества эпидемиологических наблюдений за ходом чумы, которые, по нашему мнению, вносят целый ряд новых проблем в эпидемиологию и детальной разработке которых мы надеемся в ближайшем времени посвятить специальные исследования, в настоящей работе мы ограничимся лишь сопоставлением полной хронологии чумных эпидемий с данными о солнцедеятельности.

Нижеприводимая хронологическая табл. 18 составлена на основании наиболее полных источников — специальных исторических исследований о чуме Гезера, Гирша, Геккеля, А. Дербека и др. В эту таблицу мы включили все даты о чуме, встреченные нами у перечисленных исследователей, не внося, таким образом, здесь, как и в предыдущих главах, субъективного элемента в выбор дат.

Возможно, что если бы мы попытались собрать решительно все летописные сведения об очень малых и слабых чумных эпидемиях, то у нас получился бы за несколько столетий непрерывный ряд лет, когда в одном или другом месте была отмечена чумная эпидемия, ибо чумный вирус не исчезает с лица Земли и эпидемически всегда проявляет себя, давая через известные промежутки времени эпидемические или пандемические катастрофы.

Таблица 18. Хронология чумных эпидемий и пандемий и сопоставление их с эпохами солнечной деятельности

---

---

Эпохи солнцедеятельности	Эпохи чумных эпидемий	Место распространения эпидемий
	430—425 до н. э.	Эфиопия, Ливия, Аттика
	396 до н. э.	Сицилия
	49 до н. э.	Побережье Средиземного моря
	125 н. э.	Побережье Средиземного моря
	165-168-180 н. э.	Месопотамия, Рим, Галлия и Испания
	251-266	Египет и другие страны
Макс. 502		Провансальские города
В.* макс. 514		Египет, Сирия, Персия
Макс. 535	536-542-589	Аравия, Малая Азия и Европа
В. макс.	1090-1092	Россия (Киев и окрестности)
Макс. 1129		Новгород
Макс. 1185		Новгород, Белоруссия
В. макс. 1214		Новгород
В. макс. 1225		Новгород
В. миним.	1229-1231	Россия
Макс. 1238		Псков и другие города
Макс. 1269		Россия
Макс. 1276		Россия
В. макс. 1318		Тверь
В. макс. 1334-1336		Восточный Китай
В. макс. 1348	1349-1350	Турция Испания Европа и Азия
Макс. 1353	1352-1353	Средняя Россия
В. макс.		Брабант Многие страны Европы Италия (Фл