10. Написать выражение для нормальной плотности вероятности р2(x,y) двумерной случайной величины (Х,Y), если 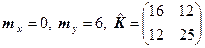
Литература
1. Боровков А.А. Курс теории вероятностей. М: Наука, 1972.
2. В.И.Тихонов. Статистическая радиотехника. М.: Радио и Связь, 1982.
3. В.Т.Горяинов, А.Г.Журавлев, В.И.Тихонов. Статистическая радиотехника. Примеры и задачи. М.: Сов.Радио, 1980.
Практическое занятие 8.
Тема 6: d-функция Дирака.
Определения и глоссарий
Обобщенные функции, производная разрывной функции
Задания для предварительной самостоятельной подготовки
Уяснить основное свойство d-функции как фильтра, ставящего в соответствие функции ее значения в некоторых точках.
2. Привести примеры использования d-функции для задания плотностей физических величин, сосредоточенных в дискретных точках пространства.
Задачи
1. Вычислить интегралы
a) 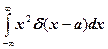 е)
е) 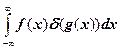
б) 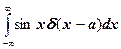 ж)
ж) 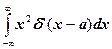
в) 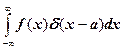 з)
з) 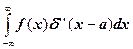
г) 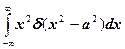 и)
и) 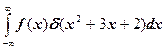
д) 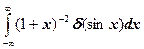 к)
к) 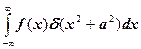
2. Найти преобразование Фурье и Лапласа от 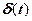 . Обсудить полученный результат.
. Обсудить полученный результат.
3. Показать, что
а) 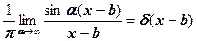 б)
б) 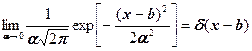
в) 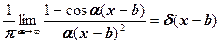 г)
г) 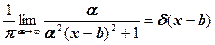
д) 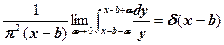
4. Разложением в ряд Фурье доказать соотношение
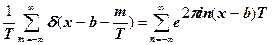
5. Используя символическое равенство 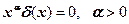 , найти общее решение уравнения
, найти общее решение уравнения 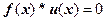 относительно неизвестной функции
относительно неизвестной функции 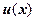 .
.
6. Закон дисперсии 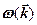 и поляризационный вектор
и поляризационный вектор  волн различной природы, способных распространяться с угловой частотой
волн различной природы, способных распространяться с угловой частотой 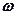 и волновым вектором
и волновым вектором 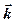 по среде передачи информации, часто получается как решение уравнения вида
по среде передачи информации, часто получается как решение уравнения вида 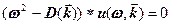 . Решить это уравнение, используя свойства d-функции, и проинтерпретировать результат.
. Решить это уравнение, используя свойства d-функции, и проинтерпретировать результат.
7. Вычислить производную функции распределения равномерно распределенной в интервале [1,5] целочисленной случайной величины.
8. Записать общее выражение для производной функции 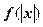 .
.
 2015-07-04
2015-07-04 347
347








