Основные расчетные зависимости для определения параметров зубчатого колеса, исходя из схемы станочного зацепления

1. Радиус окружности вершин r_a.

r_a = r + xm + h_a^*m – Δуm (1)

Δуm – уравнительное смещение инструмента (расстояние между граничной прямой инструмента и окружностью вершин заготовки).

Δу вводится в расчет для того, чтобы при создании зубчатой передачи с колесами z₁ и z₂ было бы обеспечено зацепление этих колес без бокового зазора при стандартном радиальном зазоре.

2. Радиус окружности впадин r_f.

r_f = r – h_a^*m – c^*m + xm (2)

3. Определение высоты зуба.

h = r_a – r_f = 2 h_a^*m + c^*m – Δуm (3)

4. Определение коэффициента изменения толщины зуба.

Δ=2 ^. x ^. tga

Специальные передаточные (планетарные) механизмы.

Планетарным называется механизм, имеющий в своем составе хотя бы одно звено с подвижной геометрической осью в пространстве.

Звено, имеющее подвижную геометрическую ось в пространстве, называется сателит.

Звено, на которое устанавливают ось сателитов, называется водило (Н).

Зубчатые колеса, имеющие неподвижную геометрическую ось в пространстве, называются центральными.

Центральное колесо, имеющее внешние зубья, называется солнечное колесо.

Центральное колесо, имеющие внутренние зубья, называется коронная шестерня (опорное колесо).

Достоинства планетарных передач:

1. имеют малые габариты и вес из-за того, что поток мощности, подводимый к центральному колесу, распределяется по к сателитам (к – количество сателитов). Затем поток мощности собирается на выходном звене. На одной планетарной передаче можно поставить до 24 сателитов.

2. очень высокий КПД, в среднем 0.99.

Недостатки:

Если число сателитов неравно 3, то необходим специальный механизм, который бы выравнивал нагрузку между сателитами. Этот механизм утяжеляет и удорожает конструкцию.

Сравнительный анализ передачи с неподвижными осями планетарной передачи.

На первое колесо подается крутящий момент, а со второго снимают.

Ось В неподвижна Ось В подвижна

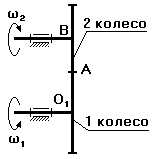
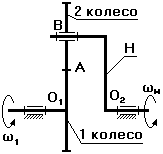
u_1-2 = 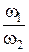= 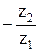u_1-Н =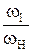

Через число зубьев u_1-Н записать нельзя, т.к. ось В – подвижная ось.

Чтобы записать передаточное отношение через число зубьев, применим метод обращения движения:

мысленно сообщим всем звеньям механизма, включая стойку, дополнительное движение с угловой скоростью -w_н. Получим обращенный планетарный механизм с неподвижными осями зубчатых колес.

В обращенном движении звенья этого механизма будут иметь следующие угловые скорости:

w₁^* = w₁ – w_Н

w₂^* = w₂ + (– w_Н) = w₂ – w_Н

w_Н^* = w_Н – w_Н = 0

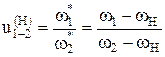- формула Виллиса

Определение передаточного отношения планетарных механизмов различных схем.

Планетарный однорядный механизм (механизм Джеймса).

КПД в одном ряду – 0.99

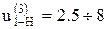
Передаточное отношение можно определить:

1. графическим способом по чертежу;

2. аналитическим способом, используя формулу Виллиса.

Графический способ определения передаточного отношения.

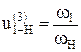
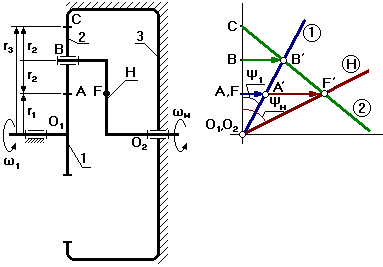
Выберем на водиле Н точку F которая расположена на том же расстоянии от оси О₂, что и точка А.

Оси О₁ и О₂ расположены на одном уровне.

Для данной схемы входное звено – звено 1 (солнечное колесо), выходным является водило Н.

Зададимся отрезком АА’, который изображает линейную скорость колеса 1 в точке А. Т.к. колесо 1 вращается вокруг О₁, то закон распределения линейной скорости по первому звену изображается прямой линией О₁А’. Сателлит 2 в т.А имеет такую же линейную скорость, что и колесо 1. В т.С сателлит 2 имеет МЦС в абсолютном движении, т.к. идет контакт с неподвижным колесом 3. Закон распределения линейной скорости по второму колесу изображается прямой линией СА’. В т.В сателлит имеет линейную скорость, которая изображается отрезком ВВ’, однако т.В является также и осью водила Н, которое вращается вокруг О₂. Следовательно, закон распределения линейной скорости по водилу изобразиться прямой линией О₂В’. Для точки F водила линейная скорость изображается отрезком FF’.

От вертикали до линии распределения скоростей по водилу измеряем угол ψ_н, а от вертикали до линии распределения скоростей по колесу 1 измеряем угол ψ₁. Т.к. углы ψ₁ и ψ_н отложены от вертикали в одном направлении, то это показывает, что входное звено 1 и выходное звено вращаются в одном направлении.

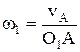
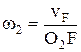
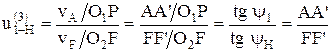
Аналитический способ определения передаточного отношения.

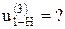
Применим метод обращения движения, обратив планетарный механизм в непланетарный.

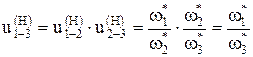
w₁^* = w₁ – w_Н

w₃^* = w₃ – w_Н = – w_Н

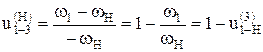
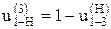
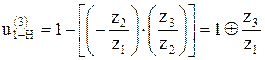– плюсовой механизм.

Планетарный механизм со смешанным зацеплением

(с одним внешним и одним внутренним зацеплением).

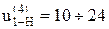при η= 0,99

Входное звено – первое звено;

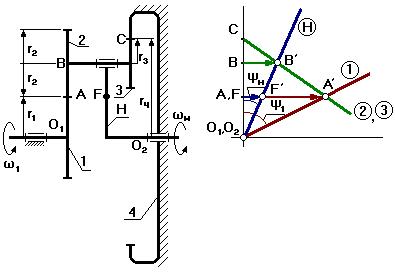Выходное – водило.

1– солнечное колесо;

2,3 – блок сателлитов;

4 – коронная шестерня;

Н – водило.

Выберем на выходном звене (на водиле) точку F так, чтобы O₁A=O₂F (O₁ и O₂ соосны).

1. Графический способ определения передаточного отношения

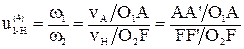
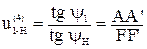
Отрезок АА' берем произвольно.

2. Аналитический способ определения передаточного отношения.

Обратим мысленно планетарный механизм в механизм с неподвижным водилом, для того чтобы использовать формулы для механизма с неподвижными осями зубчатых колес (применим метод обращения движения).

В обращенном движении каждое из звеньев будет иметь:

1 звено: ω^*₁ = ω₁ + (–ω_н)

2 звено: ω^*₂ = ω^*₃ = ω₂ + (–ω_н)

3 звено: ω^*₃ = ω^*₂ = ω₃ + (–ω_н)

4 звено: ω^*₄ = ω₄ + (–ω_н) = –ω_н

5 звено: ω^*_н = ω_н + (–ω_н) = 0

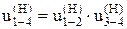(1)

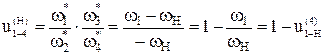
если (1) переписать через количество зубьев, то

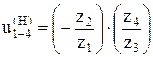
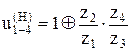
плюсовой механизм