Условие равновесия для этой системы запишется в виде

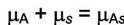
(6.1)

Выразим химические потенциалы компонентов:

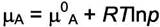
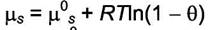
- для свободных адсорбционных центров;

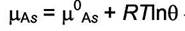
- для комплексов адсорбат - адсорбент.

- для свободных молекул адсорбата;

В этих уравнениях 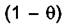выступает в качестве мольной доли свободных

центров, а 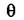- мольной доли занятых центров. Подставим значения химических потенциалов в (6.1)

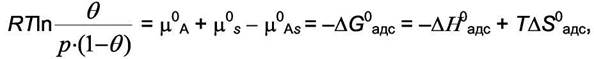
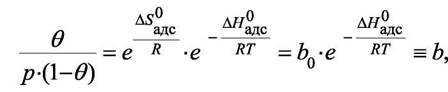
где "b" - адсорбционный коэффициент, а по смыслу константа равновесия для процесса адсорбции . Последнее уравнение удобнее разрешить относительно доли занятой адсорбируемым газом поверхности θ:

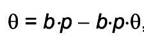
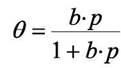
откуда

(6.2)

Уравнение (6.2) носит название уравнения Лэнгмюра.

Запишем уравнение (6.2) в другом виде, введя величину адсорбции.

По определению 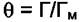и тогда

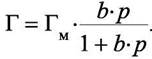
(6.3)

Из зависимости 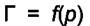можно найти величины 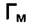и "b". Для этого

перепишем (6.3) так:

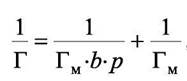
(6.4)

т. е. в координатах 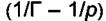будет прямая линия, тангенс угла наклона

которой равен 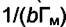, и отсекающая на оси ординат отрезок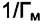

Зависимость (6.4) изображена на рис. 6.1. Обработка экспериментальных результатов в этих координатах позволяет определить величину максимальной адсорбции 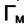и константу равновесия процесса адсорбции «b».

С ростом температуры при постоянном p величина "b" уменьшается, следовательно, и величина Г будет уменьшаться. Изотерма

Рис. 6.1 Изотерма адсорбции.

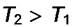пойдёт ниже, но будет стремиться к 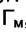, которое от Т не зависит (см. рис. 6.2).

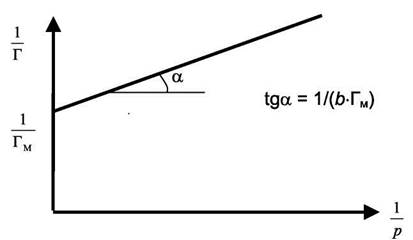
Рис. 6.2. Влияние температуры на вид изотермы адсорбции.

При малых давлениях p величина 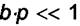, и (6.3) превращается в