2015-07-04
856
Над твёрдой поверхностью имеется смесь газов из i компонент. Обозначим θi долю поверхности s, занятой i - ым компонентом, причём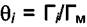 
. Согласно третьему предположению Лэнгмюра 
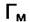одинаковы для всех газовых компонент, а 
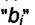- различны в основном за счёт отличия в теплотах адсорбции. Для каждого компонента имеем
|
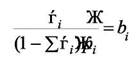
Введем понятие доли свободной поверхности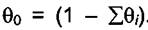 
. Тогда
уравнение Лэнгмюра запишется в виде
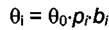
где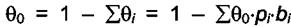 
. Из последнего уравнения можно
записать
|
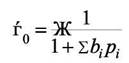
и для доли поверхности, занятой i- ым компонентом имеем
|
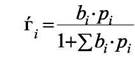
(6.6)
Формула (6.6) описывает адсорбционную конкуренцию компонент за обладание центрами адсорбции.
Величины bi могут отличаться в десятки и сотни тысяч раз. Предположим, что для двух газов адсорбционные коэффициенты отличаются в 105 раз. Тогда при равенстве b0 имеем
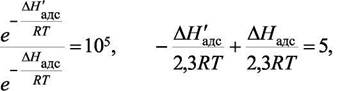
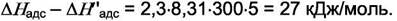
Если теплоты адсорбции отличаются на ~ 27 кДж/моль у двух газов, то их адсорбционные коэффициенты отличаются в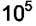 
раз.
На разнице адсорбционных коэффициентов и основана работа противогаза. Газов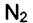 
и 
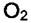в воздухе много, но их 
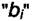на угле мало, а примеси 
, 
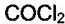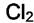в воздухе могут быть малыми, но их bi велики.
Поэтому активный элемент противогаза адсорбирует хлорсодержащие газы сильно и значительно снижает их концентрации во вдыхаемом воздухе. Газ, про который говорят, что он адсорбируется сильно, имеет
произведение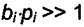 
Если газ адсорбируется слабо, это означает, что его
адсорбционный коэффициент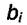 
мал и величиной 
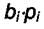в знаменателе (6.6) можно пренебречь по сравнению с остальными членами.
