2015-07-04
444
В этом вопросе можно выделить несколько различных подходов к расчёту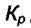 
для любой температуры Т. Сам вид уравнения
|
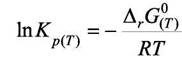
(7.13)
указывает на первую возможность такого расчёта. Так как
|
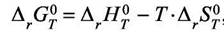
то надо знать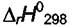 
, 
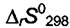и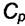 
, каждого участника реакции и можно
вычислить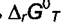 
, а затем по формуле (7.13) вычислить и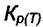 
Второй подход состоит в использовании уравнения Гиббса -Гельмгольца, записанного для реакции
|
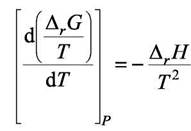
Продифференцируем (7.13) по температуре при постоянном р
|
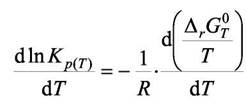
и используя уравнение Гиббса изобары Вант Гоффа:
- Гельмгольца, получим уравнение
|
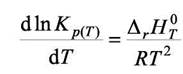
(7.14)
Если принять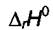 
не зависящей от температуры (небольшой диапазон температур или 
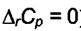ΔrСр=0), то (7.14) можно записать в интегральной форме
|
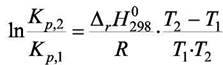
(7.15)
Уравнение (7.15) можно использовать и в случае грубых оценок Кр для любых температур, учитывая, что при больших абсолютных значениях
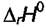слабо меняется с температурой. В таких расчётах надо знать 
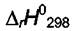и значение 
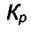при одной температуре.
Формула (7.14) даёт возможность и точного расчёта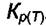 
. Надо помнить, что 
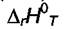включает в себя и члены с энтальпиями
конденсированных фаз, несмотря на то, что в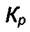 
входят только газовые компоненты. Получим эту формулу. Используем закон Кирхгофа в виде
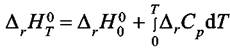
где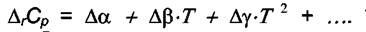 
Тогда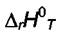 
запишется
