Стереометрические способы таксации

Форма поперечных сечений древесных стволов. Наиболее ценной частью дерева является ствол, на долю которого приходится 60-85 % объема дерева. Поэтому определение объема ствола составляет одну из главных задач лесной таксации.

Древесный ствол, как и отдельные его части, имеет некоторое сходство с правильными стереометрическими телами. Поэтому при определении объемов растущих и срубленных деревьев или частей ствола могут быть применимы законы и правила стереометрии. Формы древесных стволов весьма разнообразна. У деревьев, выросших в густом лесу, стволы более правильной формы, у одиночно растущих деревьев - обычно неправильной, при этом у них сильно развита крона.

Поперечные срезы древесных стволов, или, как принято их называть, поперечные сечения, по форме напоминают круги или эллипсы. Исследования показали, что у хвойных пород взаимно перпендикулярные диаметры в нижней части ствола в среднем различаются на 3,7 %, а в средней части ствола - на 3,1 %.

Исследованиями установлено, что определении поперечных сечений нижней части ствола по формам круга и эллипса погрешность исчисления возрастает с увеличением толщины коры. У деревьев с тонкой корой это преувеличение в среднем равно 1 %, С ТОЛСТОЙ КОРОЙ 2-3 %, с очень толстой корой - 4-5 %. При вычислении площадей поперечных сечений окоренных стволов формулы круга и эллипса дают для любого сечения по всей высоте ствола преувеличение на 0,5-1 %.

В широкой таксационной практике ошибки, не превышающие приведенные выше, считаются неизбежными. Поэтому площади поперечных сечений находят по формуле круга, обеспечивающей точность до 3 %.

Форма продольных сечений древесных стволов. Если древесный ствол разрезать по середине вертикальной плоскостью, то в сечении получится фигура, отграниченная кривой (рис.), которая расположена симметрично по отношению к вертикальной оси. При таком положении древесный ствол можно рассматривать как тело вращения, ограниченное некоторой кривой. Зная уравнение этой кривой можно определить объем ствола. Многочисленные исследования кривых ствола показали, что они неправильны и непостоянны. Уравнения, точно определяющие характер этих кривых, до сих пор не найдено.

у

О х

Рис. Продольное сечение древесного ствола

Определить объем ствола аналитически можно было бы в том случае, если бы для каждого ствола было известно уравнение его поверхности.

Отсутствие общего уравнения поверхности ствола заставляет ограничиваться методом приближенных вычислений. Степень точности получающихся при этом результатов может быть очень высокой. Она зависит от погрешностей измерений.

Для упрощения исходят из предположения, что ствол есть тело вращения. В этом случае всякое сечение ствола, перпендикулярное продольной оси, есть круг. Однако изучение поперечного сечения ствола показало, что оно не является кругом. Поэтому, рассматривая древесный ствол как тело вращения, допускают определенную условность.

Ошибки в определении объема ствола, принятого за тело вращения, не превышают допускаемой при таксации погрешности. Если ствол считать телом вращения, задачу по определению его объема можно значительно упростить.

Многочисленные исследования показали, что образующая древесного ствола - слишком сложная кривая и на всем протяжении не может быть представлена одной аналитической кривой. Правильнее ее рассматривать как сочетание разных кривых. Поэтому и древесных ствол ближе к телу, состоящему из различных конусообразных тел вращения.

В нижней части ствола образующая обычно имеет вогнутую форму, на большей части протяжения ствола она выпуклая и лишь на сравнительно коротких участках приближается к прямой.

Великий ученый Д. И. Менделеев для определения объемов применил уравнение кубической параболы, характеризующее образующую древесного ствола. Уравнение кубической параболы имеет следующий вид:

y = a + bx + cx² + dx³, где

y - полудиаметры ствола на разной высоте,

x - расстояние от шейки корня до места измерения диаметров

a, b, c, d - некоторые постоянные коэффициенты.

Приближенные формулы для определения объемов древесных стволов и их частей. Если площадь поперечного сечения ствола на уровне основания выразить через g_0, а верхнее сечение ствола g_L, то объем ствола V будет равен: g₀ + g_L

V = ^{-------------} L

Эта формула в лесной таксации называется простой формулой Смалиана.

Для определения объема ствола можно использовать другую формулу. Если поперечное сечение на середине ствола обозначить буквой g, то объем ствола будет определяться формулой:

V = g · L

Эта формула основная в лесной таксации. Она называется формулой срединного сечения, или формулой Губера. Это название она получила по фамилии автора - немецкого лесовода Губера. В основе способа лежит условное приравнивание объема ствола к объему цилиндра такой же длины и диаметра, равного диаметру на половине длины ствола.

Следовательно, для определения объема ствола надо сделать всего два измерения: определить его длину и диаметр на половине его длины (как среднеарифметическое из двух взаимно перпендикулярных измерений). По полученному диаметру определяют площадь поперечного сечения и умножают ее на длину ствола.

Наиболее точные результаты по этой формуле получается тогда, когда форма древесного ствола близка к форме цилиндра или параболоида. Для стволов более выпуклой формы, чем параболоид, формула дает несколько увеличенный результат (до 6 %), а для сильно сбежистых стволов (имеющих форму конуса) уменьшенный на 10-20 % и более. Поэтому чаще эта формула применяется для определения объемов кряжей и бревен.

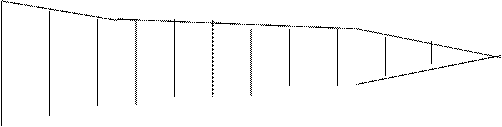
Определение объема ствола по сложной формуле срединного сечения. Допустим, что древесный ствол разделен на n отрезков длиной l (рис.).

^{L l l l l l l l l l l}

g₀ g₁ g₂ g₃ g₄ ................................... g_n-1 g_n

По формуле среднего сечения Смалиана объем ствола будет равен:

(g_{0 +} g₁) (g₁ + g₂) (g₂ + g₃)

V = V₁ + V₂ + V₃ + V₄ +...... + Vn = ^{---------------} l + ^{----------------} l + ^{-----------------} l +

2 2 2

(g₃ + g₄) (g_n-1 + g_n) 1

+ ^{----------------} l +.............. + ^{-----------------} l = ^--- (g₀ + g₁ + g₁ + g₂ + g₂ + g₃ + g₃ +

2 2 2

g_{0 +} g_n

+ g₄....+ g_n-1 + g_n) l = ^{--------------} + (g₁ + g₂ + g₃ + g₄ +..... + g_n-1) l

2

Эта формула называется сложной формулой Смалиана.

Если определить объемы отдельных отрезков по простой формуле срединного сечения Губера, то при разделении ствола на n отрезков общий объем его будет равен:

V = V₁ + V₂ + V₃ + V₄ +....... + V_n = (g₁ + g₂ + g₃ + g₄ +..... + g_n) l

Эта формула называется сложной формулой срединных сечений, или сложной формулой Губера.

В практике определения объема ствола используют отрезки одинаковой длины, обычно 2-х метровые, или 1-метровые. При делении ствола на отрезки в этом случае остается вершина длиной h. Ее объем находят по формуле объема конуса:

gh

V_вер = ^--------

3

В научных исследованиях иногда используют для определения объема ствола формулу Госфельда и Симпсона. Для определения объема ствола по формуле Госфельда необходимо измерить диаметры двухметровых отрезков в верхнем сечении каждого отрезка и на 0,67 м от их нижних сечений (р).

V = g + g + g +..... + 3 (p + p + p +.... + p) ·1/4, где

l - длина отрезка

В формуле Симпсона при определении объемов отдельных отрезков использована простая формула Ньютона-Рике

V = g₀ + g_n + 2 (g₁ + g₂ +... + g_n-1) + 4(g₁ + g₂ +... + g_n ) · l/6

Обычно эту формулу используют для нахождения площади, ограничиваемой параболой.

По всем рассмотренным формулам объем древесных стволов или их частей определяется приближенно. Объемы, определяемые ксилометрическим способом, принято считать за истинные.

Сопоставление объемов, вычисленных по сложным формулам и найденных ксилометрическим способом, показали, что все формулы дают близкие результаты.

Расхождения по всем четырем формулам лежат в пределах 2 %. С практической точки зрения их следует признать несущественными и все четыре формулы равноценны. Формулы Симпсона и Смалиана дают отклонения с положительным знаком, другие – с отрицательным.

Для практического применения наиболее удобна формула срединного сечения, предложенная Губером. Ее рекомендуют для самых точных исследований.

Определение объемов целых стволов при помощи простых формул дает менее точные результаты. Проста формула Смалиана и формула Симпсона систематически преувеличивают объемы целых стволов за счет корневых наплывов, площадь сечений которых эти формулы учитывают, но эти наплывы, как объемообразующие факторы ствола, не имеют большого значения. Как показали исследования кафедры таксации Воронежского лесохозяйственного института, простая формула Смалиана при таксации дубовых стволов дает систематическое преувеличение в среднем на 65 %, а простая формула Симпсона на 23 %.

Варьирование объемов отдельных стволов, вычисленных по простой формуле Губера, характеризуется средним квадратическим отклонением от истинного значения равным ± 12 %.

При учете отдельных деревьев необходимо измерять диаметры как можно точнее, в противном случае при вычислении объема деревьев получатся существенные ошибки.

При учете отдельных деревьев необходимо измерять диаметры как можно точнее, в противном случае при вычислении объема деревьев получатся существенные ошибки.

Достаточно простую формулу определения объема ствола предложил Н. Н. Дементьев f_ств = d²_1.3 h/3. Он принял f = 0,425 при q₂ = 0.65. Если q₂ имеет другие значения, то вводят поправку высоты, равную 3 м на каждые 0,05 коэффициента формы: со знаком «плюс» при q₂ > 0.65 и со знаком «минус» при q₂ < 0.65. Так, для ели (q₂ = 0,70) формула примет вид V_ств = d²_1.3 (h + 3)/3, а в общем виде

V_{ств =} d²_1.3 (h ± К) / 3,

где К - поправочный коэффициент. Диаметр d_1.3 берут в метрах.

Очень простую формулу для определения объема ствола применил Г. Денцин. По формуле Г. Денцина - V_ств = 0,001d²_1.3 - диаметр на высоте груди, определенный до целого числа сантиметров, возводят в квадрат, а затем в полученном значении запятую переносят на 3 знака влево. Удовлетворительные результаты по этой формуле получают при высоте сосны 30 м; ели, дуба и бука - 26 м; пихты - 25 м. Поэтому при других значениях высоты вносят поправку к объему: для сосны ± 3 %, ели и пихты ± 3-4 %, дуба и бука ±5 % (знак «плюс» используют при увеличении высоты, знак «минус» - при ее уменьшении).