Расстояние от точки до прямой

Определение. Расстоянием от точки М до прямой ℓ является длина перпендикуляра, опущенного из точки М на l прямую ℓ.

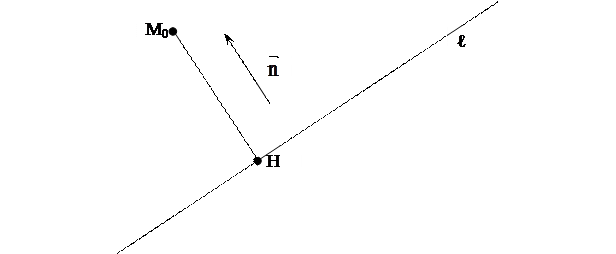
Рис.13

Теорема IV. Расстояние от точки М₀(x₀ ; y₀)прямой ℓ, заданной уравнением общего вида: ℓ: Ах+Ву+С=0, вычисляется по

формуле: .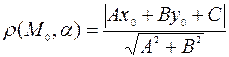

Доказательство.

Пусть в прямоугольной системе координат задана прямая ℓ: Ах+Ву+С=0 и т. М₀(x₀; y₀), не лежащая на этой прямой. Вычислим расстояние от точки М_о до прямой ℓ. Заметим,что 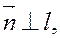=> 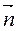|| 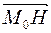, где точка Н – основание перпендикуляра, опущенного из точки М₀ на прямую ℓ, координаты которой Н(x_H; y_H).(Рис.13)

Тогда .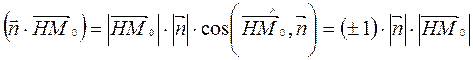

Откуда следует, что ρ(М₀,ℓ) = ǀНМ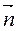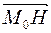ǀ= ǀ(, )ǀ/ǀ 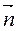ǀ. Учитывая, что(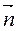, 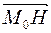)= А(x_H-x₀) +B(y_H-y₀); 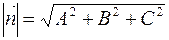и так как точка Н лежит на прямой ℓ, то есть Ах_Н + Ву_Н + С=0, получаем:

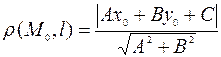(10)

Угол между двумя прямыми на плоскости.