Если точка принадлежит прямой, то проекции точки принадлежат одноименным проекциям прямой

А всегда ли чертеж позволяет судить о взаимном положении точки и прямой? Укажем три случая, когда это возможно.

1. Даны три проекции прямой и точки.

2. Даны две проекции точки и прямой общего положения.

3. Для прямой частного положения в системе двух плоскостей проекций даны проекции точки и прямой на ту плоскость, которой прямая параллельна.

 

 

 

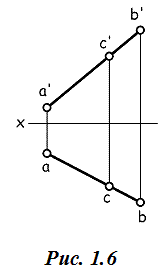
Располагая чертежом на рис. 1.6, следует утверждать, что точка С принадлежит прямой АВ, поскольку прямая АВ – прямая общего положения, а проекции c и c’ принадлежат соответственно проекциям ab и a’b’.

 

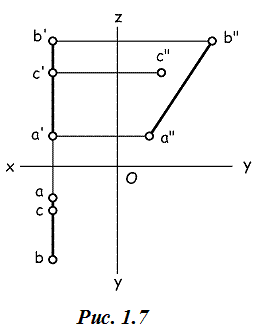Если же заданы горизонтальная и фронтальная проекции прямой АВ (рис. 1.7) и точки С, то заключение о принадлежности точки С прямой АВ было бы преждевременным: прямая АВ – прямая, параллельная профильной плоскости проекций, и для определения взаимного положения точки и прямой следует располагать профильной проекцией прямой и точки. После построения проекций a”b” и c” становится ясным, что точка С не принадлежит прямой АB.

 

 

Взаимное положение двух прямых линий

Прямые линии в пространстве могут пересекаться или не пересекаться. Непересекающиеся прямые могут быть или параллельны друг другу или не параллельны, т. е. образовывать скрещивающиеся прямые.

Пересекающиеся прямые (рис. 1.8 а) – это прямые, имеющие общую точку. Но, если точка принадлежит прямой, то проекции точки принадлежат проекции прямой. Поэтому точка общая для двух прямых должна иметь проекцию, принадлежащую как проекции одной из прямых, так и проекции другой прямой: проекции прямых должны пересекаться в точке, являющейся проекцией точки пересечения прямых в пространстве. Эти соображения приводят к чертежу на рис. 1.8 б, где изображены проекции прямых AB и CD, пересекающихся в точке М, и позволяют сформулировать следующее правило изображения подобных прямых.

 

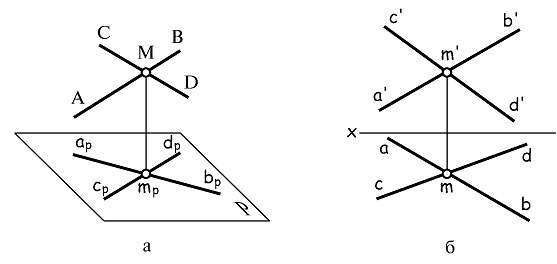
Рис. 1.8

 

Если прямые пересекаются, то пересекаются их одноименные проекции в точках, которые являются проекциями точки пересечения прямых в пространстве (и потому лежат на одной линии связи).

 

 

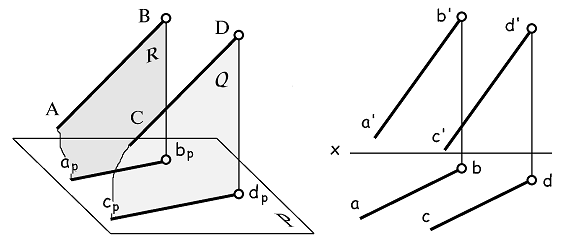
Рис. 1.9

 

Если взаимно параллельные прямые АВ и CD (рис. 1.9 а) проецировать на плоскость Р, то каждая из прямых вместе с любым из проецирующих ее лучей задает плоскость. Так прямая АВ и луч из точки В задает плоскость R, а прямая CD и луч из точки D задает плоскость Q. Плоскости R и Q параллельны между собой, поскольку выполняется признак параллельности двух плоскостей: две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости. Известно, однако, что, если две параллельные плоскости (R и Q) пересекаются третьей плоскостью (Р), то линии пересечения их взаимно параллельны. В рассматриваемом случае такими линиями пересечения являются проекции прямых АВ и CD на плоскость P, и, следовательно, a_pb_p параллельна c_pb_p

Параллельные прямые изображаются на чертеже параллельными одноименными проекциями (рис.1.9 б).

Скрещивающиеся прямые – это прямые, не лежащие в одной плоскости и не имеющие общей точки. Поэтому, хотя проекции таких прямых могут и пересекаться, но точка пересечения проекций не является проекцией одной и той же точки. Например, скрещивающиеся прямые АВ и CD (рис. 1.10 а) имеют пересекающиеся проекции a_pb_p и c_pd_p, но в точке пересечения проекций располагаются проекции двух точек: точки М, принадлежащей прямой АВ, и точки N, принадлежащей прямой CD.

 

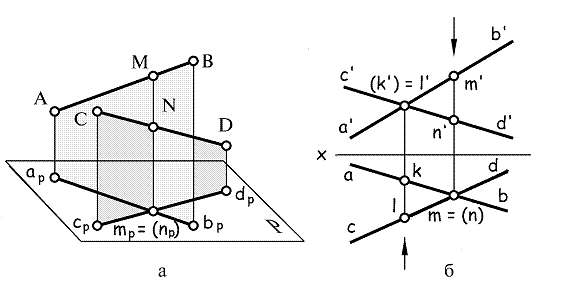
Рис. 1.10

 

Пример изображения проекций скрещивающихся прямых показан на рис. 1.10 б. Здесь пересекаются и фронтальные, и горизонтальные проекции прямых АВ и CD. В точке пересечения горизонтальных проекций прямых совпадают проекции точки М, принадлежащей прямой АВ, и точки N, принадлежащей прямой CD, а в точке пересечения фронтальных проекций совпадают проекции точки К, принадлежащей прямой АB, и точки L, принадлежащей прямойCD.

Такие точки, которые располагаются на одном проецирующем луче, называются конкурирующими. Эти точки соперничают в видимости относительно той или иной плоскости проекций. На рис. 1.10 а точки М и Nявляютcя конкурирующими относительно плоскости Р. Очевидно, что видна будет точка М, поскольку она находится дальше от плоскости Р и, следовательно, ближе к наблюдателю, чем точка N (точка N закрыта точкой М).

Для определения видимости конкурирующих точек М и N (рис. 1.10 б) относительно горизонтальной плоскости проекций следует выяснить их положение относительно плоскости Н. Из взаимного положения фронтальных проекций m' и n' следует, что точка M расположена выше (и, следовательно, ближе к наблюдателю), чем точка N. Поэтому точка М видна, а точка N, расположенная под точкой М, не видна. К аналогичному заключению можно прийти, если использовать направление взгляда на горизонтальную плоскость, показанное стрелкой.

Для определения видимости конкурирующих точек К и L относительно фронтальной плоскости проекций следует выяснить их положение относительно плоскости V. Из взаимного положения горизонтальных проекций k и l следует, что точка L расположена дальше от плоскости V (и, следовательно, ближе к наблюдателю), чем точка К. Поэтому точка L видна, а точка К, расположенная за точкой L не видна. К такому же выводу можно прийти, используя направление взгляда на фронтальную плоскость проекций, показанное стрелкой.

Мы рассмотрели особенности изображения на чертеже прямых, расположенных в пространстве различным образом друг относительно друга. Однако судить по чертежу о взаимном расположении прямых в пространстве можно лишь в следующих случаях.

1. Даны три проекции прямых.

2. Даны две проекции прямых общего положения.

3. Если хотя бы одна из прямых является прямой частного положения, то в системе двух плоскостей проекций дана проекция на ту плоскость, которой прямая параллельна.

Поясним последнее положение чертежом на рис. 1.11. Пусть даны фронтальные и профильные проекции прямых АВ и CD. Одноименные проекции этих прямых пересекаются, и точки пересечения проекций лежат на одной линии связи. Однако суждение на основании этих признаков о взаимном положении прямых АB и СD было бы преждевременным: прямая АВ является горизонтальной прямой, и для определения взаимного положения прямых следует располагать горизонтальными проекциями прямых АB и CD. После построения проекций ab и cd следует сделать вывод: АB и CD – скрещивающиеся прямые а точки пересечения фронтальных и профильных проекций – проекции конкурирующих точек.

 

 

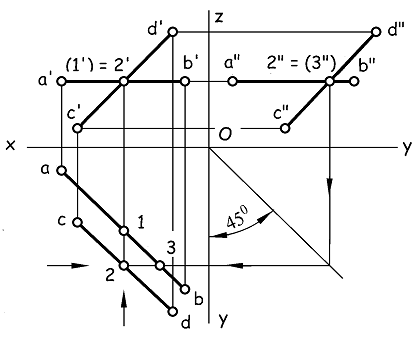
Рис. 1.11

 

 

1.4. О проекциях плоских углов. Теорема о частном случае проецирования прямого угла.

 

Отметим два очевидных предельных случая проецирования плоских углов. Если плоскость угла параллельна плоскости проекций, то любой угол проецируется без искажения. Если плоскость угла перпендикулярна к плоскости проекций, то угол проецируется в прямую. В промежутке между этими предельными положениями в зависимости от расположения сторон угла относительно плоскостей проекций любой угол может проецироваться в любой: острый угол может проецироваться в острый и тупой, а тупой угол – в тупой и острый. И лишь один из углов, а именно прямой угол, обладает чрезвычайно важной особенностью проецирования.

Если плоскость прямого угла не перпендикулярна к плоскости проекций, а хотя бы одна из сторон угла параллельна этой плоскости, то прямой угол проецируется на нее в виде прямого же угла.

 

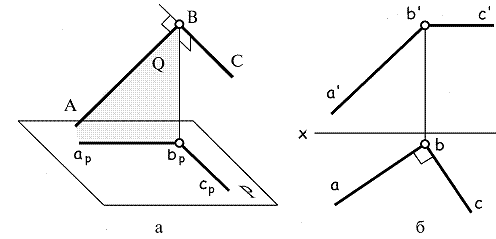
Рис. 1.12

 

Пусть угол АВС = 90⁰, а сторона ВС параллельна плоскости проекций Р (рис. 1.12 а). Выясним, чему равна его проекция a_pb_pc_p?

Рассмотрим взаимное положение стороны ВС и плоскости Q, задаваемой стороной АВ и проецирующей прямой Bb_p. [BC) ^ (AB] по условию, и [BC)^[Bb_p], поскольку [BC)ïïР, а [Bb_p]^P. Поэтому по признаку перпендикулярности прямой и плоскости [BC)^Q.

Сторона [BC) и ее проекция [ b_pc_p ) лежат в одной плоскости, определяемой лучом [BC) и проецирующей прямой [Bb_p]. При этом [ВС)ïïP. Поэтому [BС) çç [b_pc_p). Следовательно [b_pc_p)^Q. Но, если прямая перпендикулярна к плоскости, то она перпендикулярна к любой прямой, лежащей в этой плоскости, и, в частности, [b_pc_p) ^ (a_pb_p], т.е. угол a_pb_pc_p= 90⁰.

 

Наряду с формулировкой теоремы, приведенной выше, используют и другую формулировку.