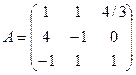 ,
,
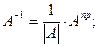
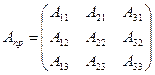 ,
,
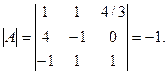
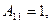
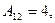
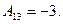
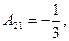
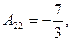
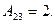
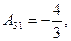
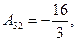
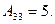
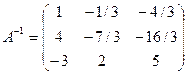 ;
; 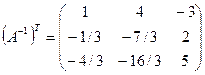 ;
;
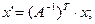
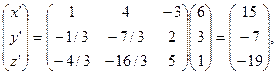
значит координаты 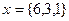 относительно базиса
относительно базиса 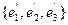 будут
будут 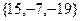 .
.
. Вычислить площадь параллелограмма, построенного на векторах 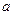 и
и 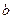 .
.
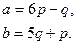
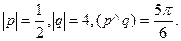
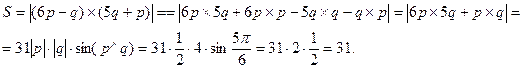
4.. Вычислить объем тетраэдра с вершинами в точках 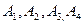 и его высоту, опущенную из вершины
и его высоту, опущенную из вершины 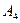 на грань
на грань 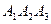 .
.
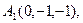
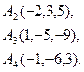
Решение.
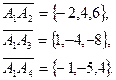
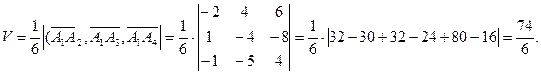
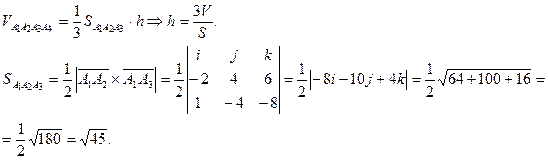
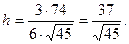
5. Найти расстояние от точки 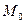 до плоскости, проходящей через точки
до плоскости, проходящей через точки 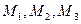 .
.
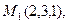
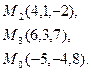
Решение.
Уравнение плоскости, проходящей через 3 точки
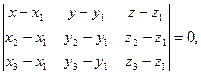
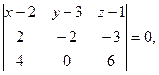
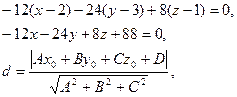
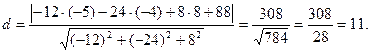
6. Написать уравнение плоскости, проходящей через точку 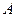 перпендикулярно вектору
перпендикулярно вектору 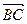 .
.
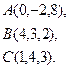
Решение.
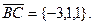
Т.к. вектор 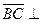 искомой плоскости, то его можно взять в качестве вектора нормали, следовательно
искомой плоскости, то его можно взять в качестве вектора нормали, следовательно
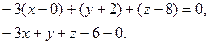
Найти точку пересечения прямой и плоскости.
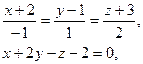
 2015-07-02
2015-07-02 447
447








