Задача 12

Условие задачи. На статически неопределимую раму с высоты h падает груз Q (рис. 28). Требуется подобрать размеры элементов рамы, выполненных из стали в виде круглого поперечно-

го сечения, если: 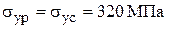, а коэффициент запаса прочности стержней n = 2. Массу упругой системы не учитывать.

Данные для решения задачи взять из табл. 13.

Порядок решения задачи показан на примере.

Пример. Подобрать диаметр стержней статически неопределенной рамы, изготовленных из стали (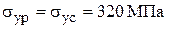). На

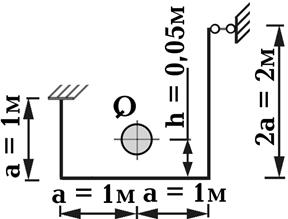раму с высоты h = 0,05 м падает груз Q = 600Н (рис. 29). Коэффициент запаса прочности принять n = 2; модуль упругости стали Е = 2×10⁵ МПа. Массу упругой системы не учитывать.

Решение. Напряжения, возникающие при ударе, найдем по формуле

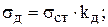
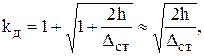
где s_ст – напряжения от статического приложения груза Q;

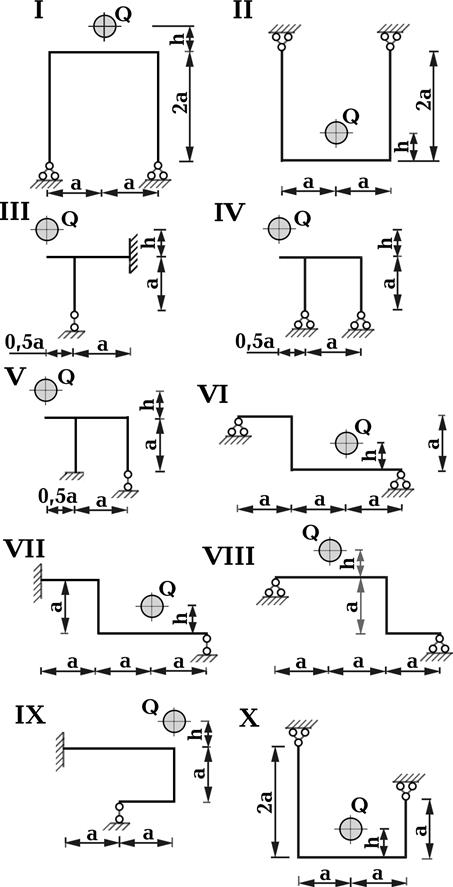
Рис. 28.

Таблица 13

№ строки	Расчетная схема	а, мм	h, мм	Q, Н
	I	2,1
	II	2,2
	III	2,3
	IV	2,4
	V	2,5
	VI	2,6
	VII	2,7
	VIII	2,8
	IX	2,9
	Х	3,0
	е	д	е	г

k_д – динамический коэффициент;

D_ст – прогиб в заданной системе от статически приложенного груза

Q в направлении удара.

Для определения напряжений необходимо сначала раскрыть статическую неопределимость рамы, а затем построить эпюры внутренних усилий.

1). На раму наложены четыре связи, система плоская и можно использовать три уравнения равновесия, следовательно, заданная система один раз статически неопределима, то есть

.

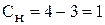2). Выберем один из вариантов основной системы метода сил, отбрасывая правую связь и сохраняя заделку.

Основную систему нагрузим статически приложенной нагрузкой Q и основным неизвестным Х₁ вместо отброшенной связи (рис. 30,а).

3). Для основной системы запишем каноническое уравнение метода сил

.

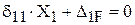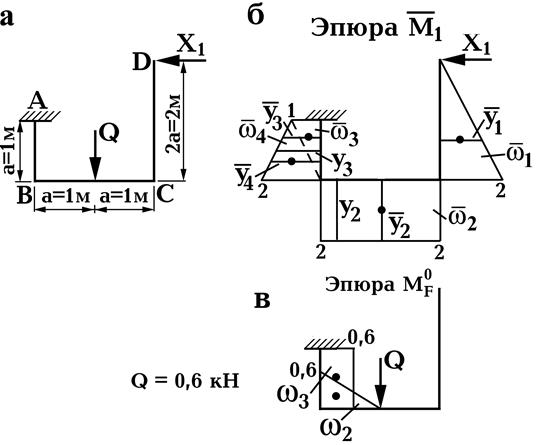Рис. 30

4). Для определения коэффициентов d₁₁ и D_1F строим в основной системе эпюры изгибающих моментов: от единичной силы 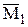и от заданной нагрузки 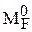(рис. 30,б, в).

5). Определим перемещения d₁₁ и D_1F, вычисляя интеграл Максвелла-Мора способом Верещагина

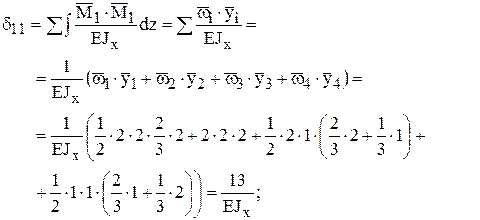
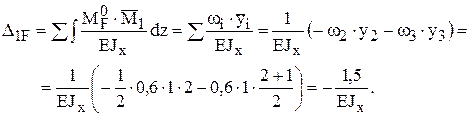
6). Решая каноническое уравнение, получим

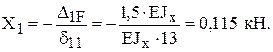
Знак "плюс" у Х₁ означает, что направление Х₁ было выбрано правильно.

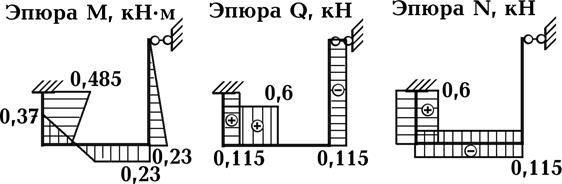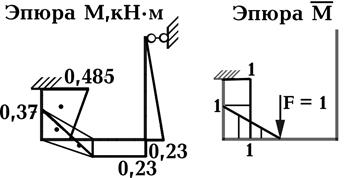
7). Определим внутренние усилия методом сечений и построим эпюры изгибающих моментов, поперечных и продольных сил (рис. 31).

Рис. 31.

8). Выполним деформационную проверку, определяя перемещение в направлении опорной реакции Х₁для заданной системы.

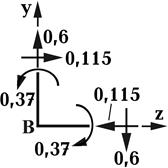
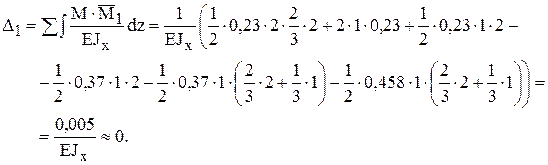
Правильность построения эпюр Q и N проверим, вырезая узлы и рассматривая их равновесие. Например, вырезая узел "В" и подставляя усилия Q и N, взятые с эпюр, имеем:

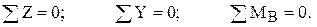
9). Подберем ориентировочное значение диаметра стержней рамы из условия прочности при статическом нагружении для сечения, в котором изгибающий момент максимален ().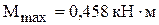

Полагаем, что

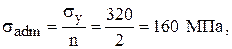
тогда

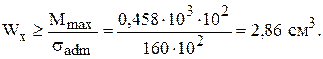
Так как

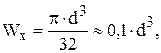
то

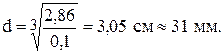
Учитывая динамический характер приложения нагрузки, увеличиваем диаметр стержней рамы на 45%. Окончательно примем

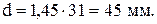
Тогда

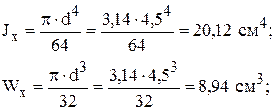
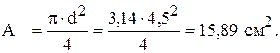
10). Определим статическое перемещение (прогиб) D_стприкладывая единичную силу 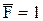в направлении удара в основной системе метода сил и перемножая эпюры изгибающих моментов М и 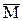(рис. 32):

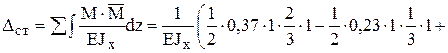
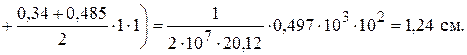
11). Определим динамический коэффициент

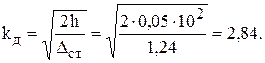
12). Проверим условие прочности в сечении с максимальным моментом 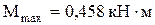и продольной силой 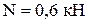, то есть в наиболее опасной точке

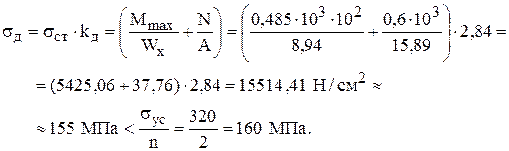
Следовательно, прочность рамы обеспечена.