Корреляционный анализ исходных данных

Анализ матрицы парных коэффициентов корреляций [1]

Чтобы получить матрицу парных коэффициентов корреляции, нажмите кнопку табличных опций, затем выберите Correlations. На экране появится таблица корреляций (рисунок 11).

Рисунок 11 – Матрица парных коэффициентов корреляции

В данной таблице информация представлена в виде групп, состоящих из трёх чисел, первое число ─ коэффициент корреляции Пирсона, второе ─ число наблюдений, третье - расчётное значение уровня значимости (р-value) для статистик Стьюдента.

Анализ матрицы парных коэффициентов корреляций преследует решение двух задач: 1) выявление значимых независимых переменных; 2) выявление мультиколлинеарности независимых переменных.

Корреляционная матрица (рисунок 11) симметрична относительно главной диагонали, рассмотрим её верхнюю часть.

Последний столбец содержит коэффициенты между зависимой переменной у и независимымипеременными х₁, х₂, х_{3 .} Проанализируем коэффициенты данного столбца для выявления значимых независимых переменных.

Все коэффициенты 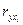отличны от нуля, т.е. 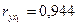, , 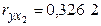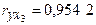. Возникает вопрос, объясняется ли это действительно существующей линейной корреляционной связью между переменными х_i и у в генеральной совокупности или является следствием случайности отбора значений переменных в выборку.

Для каждого коэффициента корреляции проверим гипотезу Н₀: 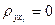, об отсутствии линейной корреляционной связи между переменными х _i и у в генеральной совокупности, при конкурирующей гипотезе Н₁: .

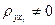Для этого рассчитаем t -статистику по формуле .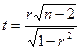

Сравним полученное расчётное значение t -статистики с табличным значением 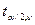, определяемого по таблице критических точек распределения Стьюдента (приложение Б) с n = n – 2 степенями свободы и заданным уровнем значимости 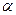(для двусторонней критической области). Если 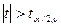, то гипотеза Н₀ отвергается, т.е. коэффициент корреляции значимо (существенно) отличается от нуля, переменная х_i значимо влияет на зависимую переменную, в противном случае Н₀ не отвергается, т. е. коэффициент незначим, а соответствующая независимая переменная незначимо влияет на зависимую переменную.

Проверим гипотезу 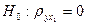при конкурирующей гипотезе Н₁: .

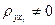Выборочный коэффициент 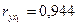(рисунок 11), поскольку 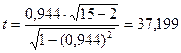> 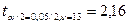, принимается гипотеза Н₁: 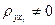, коэффициент корреляции 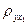между квартальным объёмом реализации у и величиной расходов на рекламу х₁ значимо отличен от нуля, что подтверждает наличие линейной корреляционной зависимости между этими переменными в генеральной совокупности.

Аналогично проверьте гипотезы о значимости коэффициентов корреляци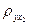и и .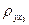

Для проверки гипотезы о значимости коэффициента корреляции можно воспользоваться расчётным значением уровня значимости р-value (р-величина) статистик Стьюдента, если р-value больше фиксированного уровня значимости 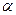, то нулевая гипотеза Н₀: 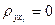не отклоняется, т.е. линейная корреляционная связь между соответствующими переменными отсутствует. В противном случае принимается альтернативная гипотеза Н₁: 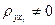, т.е. коэффициент корреляции значимо отличен от нуля.

В нашем случае р-value, равное 0,000 (рисунок 11), меньше 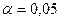принимается Н₁: .

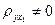О степени тесноты связи можно судить по значению коэффициента корреляции, используя шкалу Чеддока (таблица 2).

Таблица 2 – Шкала Чеддока

Проведя анализ столбца коэффициентов корреляции между зависимой переменной у и независимыми переменными х_1, х_2, х₃, установили, что значимыми являются переменные х₁ и х₃,незначимой х₂.

Для выявления мультиколлинеарности среди независимых переменных проанализируем коэффициенты корреляции 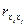. Тот факт, что 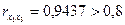, свидетельствует о том, что независимые переменные х₁ и х₃ коллинеарные, при моделировании зависимости объёма реализации продукции одну из двух переменных х₁ или х₃ исключают. При этом какую переменную оставить, а какую удалить из анализа решают в первую очередь на основании экономических соображений. Если с экономической точки зрения ни одной из переменных нельзя отдать предпочтение, оставляют ту из двух переменных, которая имеет больший коэффициент корреляции с зависимой переменной.