Сравнительный анализ матрицы частных коэффициентов корреляции с матрицей парных коэффициентов корреляции

Если переменные коррелируют друг с другом, то на величине парного коэффициента корреляции может сказываться влияние других переменных. В связи с этим возникает необходимость исследовать частную корреляцию между двумя переменными при исключении влияния остальных (m – 2) переменных.

Для получения матрицы частных коэффициентов корреляции в рабочем окне нажмите кнопку табличных опций и выберите Partial correlations (рисунок 12).

Рисунок 12 – Матрица частных коэффициентов корреляции

Проведём сравнительный анализ матрицы частных коэффициентов корреляции (рисунок 12) с матрицей парных коэффициентов корреляции (рисунок 11).

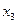Сравнивая частные коэффициенты корреляции с соответствующими парными коэффициентами, видим, что за счёт «очищения связи» коэффициенты корреляции между у (объёмом реализации за квартал) и независимыми переменными х_i подверглись изменению, связь между у и х₁, у и х₃ ослабла, теснота связи между у и х₂ существенно не изменилась_. Следовательно, переменные х₂ и , х₂ и 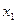соответственно усиливали влияние факторов 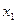и 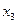на переменную 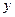, а переменные 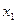и 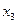не оказывали существенного влияния на тесноту связи между 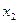и .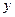

Т.к. 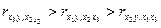, то по силе влияния на переменную 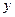порядок факторов таков 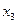, , 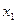х_2.