Задача об оптимальных назначениях

Рассмотрим задачу нахождения наилучшего способа назначе­ния людей на работу, при котором будет достигнута максималь­ная суммарная производительность. Задача может быть интерпре­тирована в различных вариантах. Например, под видами работ можно понимать различные изделия, строительные площадки и т.д. Работы могут выполняться людьми, станками, механизмами, при­способлениями.

Рассмотрим простейший вариант задачи о назначениях. Пусть имеется п видов работ 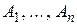и т лиц, способных выпол­нять данные работы 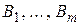производительность которых 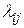. Например, 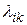означает производительность 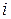-го лица при выпол­нении 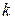-ой работы. Требуется определить оптимальное назначение людей на работы, при котором будет достигнута максимальная суммарная производительность. При такой интерпретации задачи важно, чтобы одновременно на каждый вид работы было назначе­но только одно лицо.

Рассмотрим случай, когда количество работ равно числу лиц, занятых их выполнением, т.е. т=п. Положим

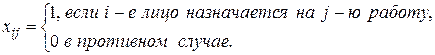(1)

Так как (по предположению) каждое лицо можно назначать только на один вид работы, то

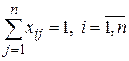. (2)

Так как каждая работа предназначается только для одного лица, то

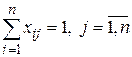(3)

Неотрицательные переменные 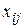принимают только два зна­чения, а именно: 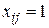, если i -e лицо используется для выполнения j -й работы, и 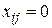, если i -е лицо не используется при выполнении j -й работы.

Суммарная производительность выразится так:

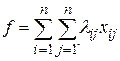. (4)

Итак, математически задача о назначениях формулируется в следующем виде. Даны системы ограничений (2) и (3) при условии (1). Требуется найти переменные 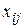, удовлетворяющие системам (2), (3) и обращающие целевую функцию (4) в максимум.

Решать задачу о назначениях можно теми же методами, ка­кими решается транспортная задача.