Опр. уравнение 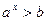 (где
(где 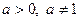 ), называется простейшим показательным неравенством. Для его решения необходимо представить правую часть следующим образом:
), называется простейшим показательным неравенством. Для его решения необходимо представить правую часть следующим образом: 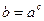 , тогда мы получим:
, тогда мы получим: 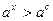 . Теперь можно перейти к неравенству относительно степеней, причем если
. Теперь можно перейти к неравенству относительно степеней, причем если 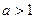 , то знак неравенства не меняется, если
, то знак неравенства не меняется, если 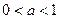 , то знак меняется на противоположный.
, то знак меняется на противоположный.
Прим.1: 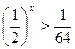
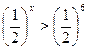
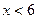
Отв.: 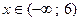 .
.
В общем случае любое показательное неравенство нужно привести к виду: 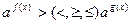 (обратить внимание, что в уравнении слева и справа только одно слагаемое и нет ни каких коэффициентов), после чего перейти к неравенству относительно степеней:
(обратить внимание, что в уравнении слева и справа только одно слагаемое и нет ни каких коэффициентов), после чего перейти к неравенству относительно степеней: 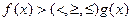 .
.
Прим.2: 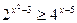
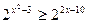
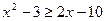
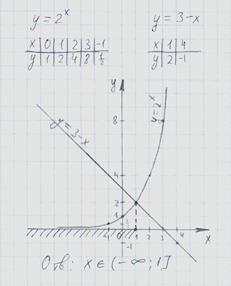
Пример графического решения неравенства:
Прим.3: 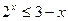
Вводим две функции: 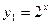 и
и 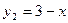 . Построим их на одной координатной плоскости:
. Построим их на одной координатной плоскости:
1. Решить неравенство 1) 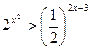 ; 2)
; 2) 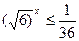
3) 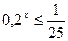 ; 4)
; 4) 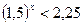 ;
;
5) 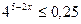 ;
;
 2015-07-03
2015-07-03 183
183







