Задачи для самостоятельного решения

1. Интегральная функция распределения случайной величины Х имеет вид:

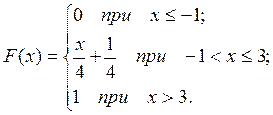
Найти: а) вероятность того, что случайная величина примет значение в интервале (0, 2); б) построить график интегральной функции распределения вероятностей. Проиллюстрировать решение графически.

2. Интегральная функция распределения случайной величины Х имеет вид:

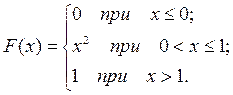
Найти: а) дифференциальную функцию распределения; б)вероятность того, что случайная величина примет значение в интервале (0,5; 1), меньше 0,5, равное 0,5; в) математическое ожидание, г) дисперсию; д) построить графики f (x) и F(х). Проиллюстрировать решение задачи графически.

3. Дифференциальная функция распределения случайной величины Х имеет вид:

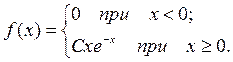
Найти: а) параметр С; б) вероятность того, что случайная величина попадет в интервал (2, 3).

4. Дифференциальная функция распределения случайной величины Х имеет вид:

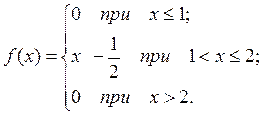
Найти интегральную функцию распределения; математическое ожидание, дисперсию и среднее квадратическое отклонение.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Дайте определение непрерывной случайной величины.

2. Что называется законом распределения непрерывной случайной величины?

3. Дайте определение дифференциальной и интегральной функции распределения вероятностей.

4. Сформулируйте свойства дифференциальной функции (плотности) распределения вероятностей непрерывной случайной величины.

5. Сформулируйте свойства интегральной функции распределения вероятностей непрерывной случайной величины.

6. Чему равны числовые характеристики непрерывной случайной величины?

7. Как можно найти вероятность попадания непрерывной случайной величины Х в заданный интервал (α, β)?

8. Приведите примеры непрерывных случайных величин.

ЛИТЕРАТУРА

1. Гмурман В.С. Теория вероятностей и математическая статистика. -7-е изд., стер. -М.: Высш. шк. 2001.-479 с.

2. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. -5-е изд., стер.– М.: Высш. шк. 2001. -400 с.

3. Колде Я.К. Практикум по теории вероятностей и математической статистике. – М.: Высш. шк., 1991. -157 с.

4. Кремер Н.Ш. Теория вероятностей и математическая статистика. -М.: ЮНИТИ-ДАНА, 2001. -543 с.

5. Егорова Ю.Б., Мамонов И.М., Корниенко Л.И. Дискретные случайные величины. Методические указания к практическим занятиям по дисциплине «Высшая математика». – М.: Издательский центр МАТИ, 2005. – 20 с.

ОГЛАВЛЕНИЕ

Введение…………………………………………………............ 3

1. Способы задания закона распределения непрерывной

случайной величины……….……………………..........…………...3

2. Числовые характеристики непрерывной случайной

величины.………………………………............................................6

3. Задачи для самостоятельного решения…………………………9

4. Контрольные вопросы………………………………………........10

Литература…………………………………………………..........10

Юлия Борисовна Егорова

Игорь Михайлович Мамонов

НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ