2.1. Математическое ожидание:

2.2. Дисперсия:
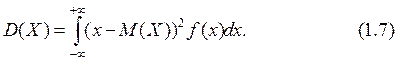
Все свойства математического ожидания и дисперсии, рассмотренные для дискретных случайных величин, справедливы и для непрерывных величин.
2.3.Среднее квадратическое отклонение:

2.4. Мода Мо (рис. 1, б) – наиболее вероятное значение случайной величины, т.е. это значение, имеющее наибольшую плотность распределения вероятности f(х).
2.5. Медиана Ме – значение случайной величины, для которого
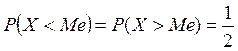
или для которого интегральная функция распределения равна ½ (рис. 1, а):
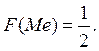
Геометрически вертикальная прямая х=Ме делит площадь под кривой распределения пополам (рис. 1, д).
2.6. Коэффициент ассиметрии А характеризует симметричность (скошенность) кривой распределения:
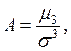
где μ3 – центральный момент третьего порядка:
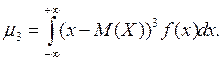
Если кривая распределения симметрична относительно математического ожидания, то А =0 (рис. 1, б-г). Если коэффициент ассиметрии А >0, то кривая распределения имеет правостороннюю ассиметрию; если А <0 – левостороннюю ассиметрию.
2.7. Коэффициент эксцесса ε и эксцесс Е характеризует островершинность (крутизну) кривой распределения:
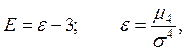
где μ4 – центральный момент четвертого порядка:
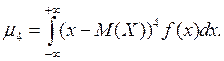
Если Е =0, то кривая распределения имеет нормальную крутизну (рис. 1, б-г). Если Е >0, то кривая распределения более островершинная по сравнению с нормальной; если Е <0 – более плосковершинная.
ПРИМЕР 1. Интегральная функция распределения случайной величины Х имеет вид:
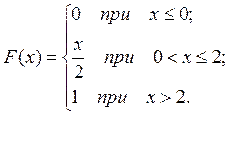
Найти: а) вероятность того, что случайная величина примет значение в интервале (1, 3); б) плотность распределения вероятностей.
РЕШЕНИЕ.
а) По формуле (1.1) получим:
Р(1<Х<3)=F (3)- F (1) = 1-1/2=1/2.
б) Плотность распределения вероятностей определим по формуле (1.2):
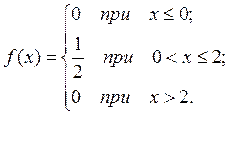
ПРИМЕР 2. Дифференциальная функция распределения случайной величины Х имеет вид:
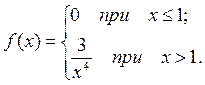
Найти: а) интегральную функцию распределения; б) вероятность того, что случайная величина примет значение в интервале (2, 3).
РЕШЕНИЕ. а) Интегральную функцию распределения найдем по формуле (1.5). Если 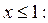
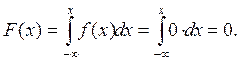
Если 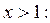
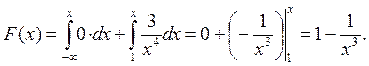
Таким образом:
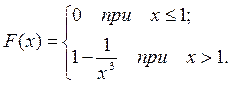
б) Вероятность того, что случайная величина примет значение в интервале (2, 3), можно найти двумя способами.
По формуле (1.1):
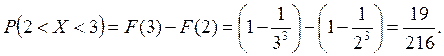
Или по формуле (1.3):
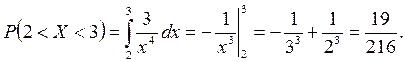
 2015-07-04
2015-07-04 679
679








