2015-07-04
2310
Число Пи
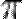(произносится «пи») — математическая константа, равная отношению длины окружности к длине её диаметра. Обозначается буквой греческого алфавита «пи». Старое название — лудольфово число.
Трансцендентность и иррациональность
· 
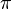— иррациональное число, то есть его значение не может быть точно выражено в виде дроби m/n, где m и n — целые числа. Следовательно, его десятичное представление никогда не заканчивается и не является периодическим. Иррациональность числа 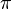была впервые доказана Иоганном Ламбертом в 1761 году путём разложения числа 
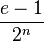в непрерывную дробь. В 1794 году Лежандр привёл более строгое доказательство иррациональности чисел 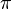и 
.
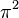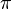· — трансцендентное число, то есть оно не может быть корнем какого-либо многочлена с целыми коэффициентами. Трансцендентность числа 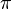была доказана в 1882 году профессором Кёнигсбергского, а позже Мюнхенского университета Линдеманом. Доказательство упростил Феликс Клейн в 1894 году.
· Поскольку в евклидовой геометрии площадь круга и длина окружности являются функциями числа 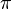, то доказательство трансцендентности 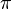положило конец спору о квадратуре круга, длившемуся более 2,5 тысяч лет.
· В 1934 году Гельфонд доказал трансцендентность числа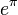 
. В 1996 году Юрий Нестеренко доказал, что для любого натурального 
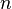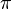числа и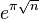 
алгебраически независимы, откуда, в частности, следует трансцендентность чисел 
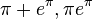и .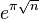
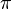· является элементом кольца периодов (а значит, вычислимым и арифметическим числом). Но неизвестно, принадлежит ли 
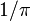к кольцу периодов.
Впервые обозначением этого числа греческой буквой 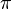воспользовался британский математик Джонс в 1706 году, а общепринятым оно стало после работ Леонарда Эйлера в 1737 году.
Это обозначение происходит от начальной буквы греческих слов περιφέρεια — окружность, периферия и περίμετρος — периметр.
История числа 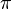шла параллельно с развитием всей математики. Некоторые авторы разделяют весь процесс на 3 периода: древний период, в течение которого 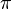изучалось с позиции геометрии, классическая эра, последовавшая за развитием математического анализа в Европе в XVII веке, и эра цифровых компьютеров.
