Метод наискорейшего подъема (для самостоятельного изучения)

Рассмотрим случай поиска безусловного экстремума выпуклой функции max F=Z(X)

1.Выберем произвольную начальную точку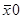

2.Подсчитаем значение функции Z(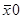) и вектора 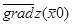(в данной точке)

3.Осуществляем движение в направлении градиента, т.е. определяем координаты новой точки 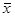, исходя из условия:

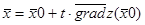
Этой формуле соответствует n координатных равенств:

x₁ = ()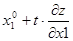

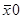x₂ = ()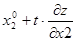

…………………………

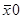x_n = ()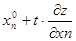

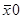4.Подсчитываем значение целевой функции в точке :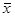

Z(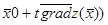 =Z(t)

(Z(t) получаем при подстановке 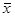в функцию Z)

5.Определяем число 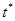, т.е. такое значение t, при котором Z(t) достигает максимума:

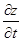= 0, отсюда находится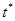

1. Полагаем 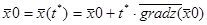и 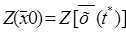, если значения функции в новой точке 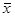оказалось больше, чем в начальной 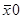, т.е. при условии:

Z(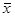)= 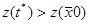заменить Z(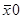) на Z().

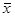Далее переходим к пункту 2.

Рассмотренный выше алгоритм предполагает, что в некоторой начальной точке 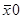определяется градиент и осуществляется движение по направлению градиента до тех пор, пока Z увеличивается. Полученная таким путем новая точка принимается за начальную и процесс продолжается.

Рассмотрим пример

Найти max z =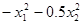

Выбираем начальную точку

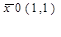
I| итерация.

1. Подсчитаем Z 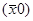и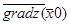

Z = -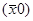

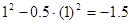
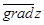= (-2х₁;-х₂)

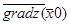=(-2;-1)

2. Осуществляем движение по градиенту:

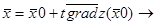
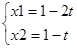
3. Z(t)=Z(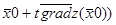 = - (1-2t) 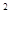- 0,5(1-t) 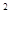= - (1-4t+4t 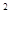) – 0,5(1-2t+t 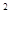) = - 4,5t 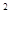+5t –1,5

-9t+5=0→ 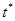= 5/9 ≈ 0,55

Проверим с помощью второй производной, будет ли точка 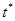точкой экстремума:

∂²Z/∂t² = -9 < 0, т.е. в точке 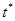- максимум.

6. Вычислим Z(t*):

Z(t*) = - 4,5∙(5/9) 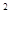+ 5∙(5/9) -1.5≈ - 4,25ּ25/81 + 25/9-1,5=

= - 1,3887 +2,78 - 1,5= - 0,1087» - 0,11;

Z(t*) > Z(); (- 0.11 > -1,5); т.е. примем точку 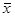за начальную 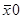, подставив в координатные равенства найденные значения

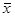(1-2·t; 1-t); 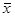(1-2·0,55; 1-0,55); 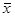(-0,1; 0,45)→ 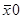= 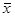(-0,1; 0,45).

Далее повторяются операции, выполненные на первой итерации, начиная с пункта 2.

II итерация.

2. Подсчитаем Z 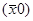и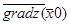

Z 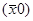=Z(- 0,1; 0,45) = - (-0,1)² – 0,5×(0,45)² = - 0,01 - 0,5×0,2025 = = - 0,01 – 0,10125» - 0,11.

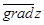
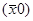= (-2х₁;- х₂) = (- 2ּ(- 0,1); - 0,45)

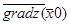=(0,2; - 0,45)

3. Осуществляем движение по градиенту:

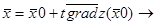
x₁ = - 0,1 + 0,2t; x₂ = 0,45 – 0,45t;

4. Z(t)=Z(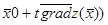 заменить 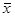на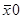

Z(t)= - (- 0,1 + 0,2t) 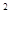- 0,5(0,45 – 0,45t) 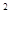=- (0,01 - 0,04t + 0,04t ) –

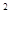- 0,5×(0,2025 - 0,405t+0,2025t 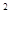) = - 0,01 + 0,04t - 0,04t 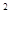- 0,10125+ +0,2025t - 0,10125t 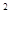= - 0,14125t 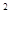+ 0,2425t – 0,11125» - 0,14t 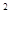+ 0,24t – 0,11.

3. Находим max Z(t): 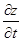= - 0,28t+0,24; → 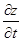= 0; →

- 0,28t+0,24 =0→ 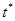≈ 0,86.

Проверим с помощью второй производной, будет ли точка 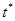точкой экстремума:

∂²Z/∂t² = - 0,28 < 0, т.е. в точке 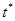- максимум.

6. Вычислим Z(t*):

Z(t*) = - 0,14×(0,86) 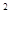+0,24×(0,86) –0,11= - 0,1035+0,2064 – 0,11 ≈ - 0,0071;

Z(t*) > Z(); (- 0,0071 > - 0,11); т.е. примем точку 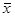за начальную 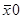, подставив в координатные равенства найденные значения

x₁ = - 0,1 + 0,2t; x₂ = 0,45 – 0,45t;

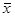(- 0,1 + 0,2t; 0,45 – 0,45t);

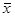(- 0,1 + 0,2ּ 0,86; 0,45 – 0,45ּ 0,86);

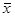(0,072; 0,063)→ 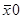= 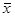(0,072; 0,063).

Далее повторяются операции, выполненные на первой итерации, начиная с пункта 2.

Процесс продолжается до нахождения точки экстремума. Он может быть конечным, тогда в точке 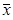* grad Z( 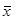*)=0 и вычисления завершаются. А может оказаться, что найдено решение с некоторой точностью ε, т.е. приближенно. В последнем случае, если за определенное число шагов (итераций) решение не будет найдено, то оптимальным считается последнее из найденных.

Замечание. Название метода связано с тем, какой экстремум ищется в задаче: если максимум целевой функции, то метод наискорейшего подъема, если минимум целевой функции, то метод наискорейшего спуска.