Метод наискорейшего спуска

Пусть дана следующая задача:

Найти min F=Z(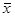) при условиях

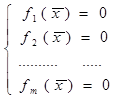
Воспользуемся для решения данной задачи градиентным методом.

1.Выбирается точка , удовлетворяющая системе ограничений (т.е. принадлежащая области допустимых решений).

2.Введем счетчик числа неудачных испытаний: S=0.

3. Подсчитывается Z(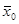) и grad Z().

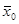Если grad Z(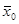)=0, то переход к пункту 11, иначе к пункту 4.

4.Осуществляется движение по градиенту, т.е.

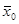= + t ·grad Z(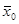) (этой формуле соответствует n координатных неравенств):

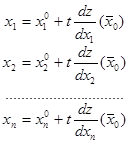
5.Подсчитаем Z(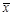)=Z(t) (при подстановке 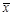в функцию Z).

6. Определяем число t* из условия minZ(t).

7. Сравним Z(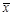)=Z(t) и Z().

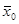Если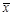 Z()> Z(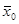), то испытание оказалось неудачным, переходим к п.8; если же испытание удачно, т.е. Z(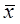)<Z(t), то проверяем, принадлежит ли новая точка области допустимых решений (ОДР). Если принадлежит, т.е. испытание удачное, то переходим к пункту 9, иначе к пункту 8.

8. Испытание оказалось неудачным S=S+1, проверяем, сколько неудачных испытаний произошло. Если S<M (заданное число неудачных итераций), то переходим к поиску следующей точки, для этого полагаем 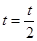и вновь подсчитываем координаты точки 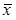(переход к пункту 7).

Если S ≥ M, то переходим к пункту 10.

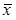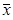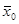9. Если испытание оказалось удачным, то найденную точку принимаем за начальную: = ; Z()=Z(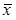) и далее переходим к пункту 3.

10. Если S 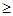M, то за заданное число итераций оптимальное решение не найдено (за конечный результат принимают в этом случае точку 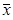последней итерации).

11. Если найдено оптимальное решение задачи в точке *,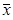

grad Z(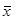 *) = 0, то вычисления завершаются.

Рассмотрим пример 17:

Найти minZ=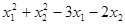

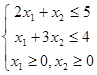
1. Выбираем точку (0;0) и проверим: принадлежит ли точка 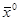(0,0) области допустимых решений?

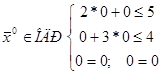Да, принадлежит.

2. S=0 (введем счетчик неудачных испытаний и зададим число таких испытаний М =5).

I итерация.

3. Подсчитаем Z()=

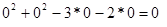
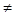и grad Z() ={2x₁-3; 2x₁-2}={-3; -2}; grad Z() = - 5 0, переходим к п. 4.

4. Осуществляем движение по градиенту:

= + t∙ grad Z()

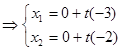
Получаем (-3t; -2t).

5. Подставляем в Z():

Z() = Z(t) = (-3t)²+(-2t)² -3(-3t)-2(-2)t = 9t²+4t²+9t+4t = 13t²+13.

6. Находим t* из условия min Z(t):

∂Z/∂t = 0; 26t+13 = 0; t*= - 13/26; t* = - 0,5.

∂²Z/∂t² = 26 > 0, то есть в точке при t* - минимум целевой функции.

7. Находим Z(t*) = 13· (- 0,5)² + 13· (-0,5) =3,25 – 6,5 = - 3,25,

Z(t*)< Z() (-3,25<0), то есть испытание удачное, S=0.

Определяем координаты точки = (-3t; -2t) = (-3·(-0,5); - 2· (-0,5)); (1,5; 1).

Подсчитаем Z() = Z(t) = - 3,25.

Проверим: принадлежит ли точка (1,5; 1) области допустимых решений?

2·1,5 + 1≤ 5? →4<5

1,5 + 3·1≤ 4? →4,5>4

1,5≥0; 1≥0.

Как видим, (1,5; 1) не принадлежит ОДР, т.е. испытание оказалось неудачным, переходим к п. 8.

8. S=S+1; S=0+1=1. Так как S<M (1<4), то полагаем t*= t*/2 = - 0,5 / 2; t*= - 0,25, переходим к п. 7.

7. Находим Z(t*) = 13· (- 0,25)² + 13· (-0,25) =0,8125 – 3,25 =- 2,4375,

Z(t*)< Z() (-2,4375<0), то есть испытание удачное, S=1.

II итерация.

1. Определяем координаты точки :

(-3t; -2t) = (-3·(-0,25); -2· (-0,25)) = (0,75; 0,5);

(0,75; 0,5).

2. Проверим: принадлежит ли точка (0,75; 0,5) области допустимых решений?

2·0,75 + 0,5≤ 5? →2<5

0,75 + 3·0,5≤ 4? →2,25<4

0,75≥0; 0,5≥0

(0,75; 0,5) принадлежит ОДР, т.е. испытание оказалось удачным (S=S+0; S=1). S=1+0;

S=1. Так как S<M (1<4), определяем = 0,75; 0,5) то переходим к п. 3.

3. Z() = Z() = Z(t) = -2,4375.

III итерация.

3. Подсчитаем

grad Z() ={2x₁-3; 2x₁-2} = {2·0,75-3; 2·0,5-2} = {-1,5; -1} = - 2,5 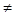0, переходим к п. 4.

4. Осуществляем движение по градиенту:

= + t* grad Z(); х₁=0,75+t·(-1,5); х₂=0,5+t·(-1)

Получаем (0,75 - 1,5t; 0,5 - t).

5. Подставляем в Z():

Z()=Z(t)=(0,75- 1,5t)²+(0,5- t)² –3(0,75- 1,5t)-2(0,5 - t)= 2,25t²+t²-2,25t -t+4,5t+2t+0,5625+0,25-2,25-1=3,25t²+3,25t - 2,4375.

6. Находим t* из условия min Z(t):

∂Z/∂t = 0; 6,5t+3,25 = 0; t*=-3,25/6,25; t* = - 0,5.

∂²Z/∂t² = 6,5 > 0, то есть в точке при t* - минимум целевой функции.

7. Находим Z(t*) = 3,25t²+3,25t - 2,4375 = 3,25· (- 0,5)² +3,25·(-0,5) - 2,4375; 3,25·0,25 +3,25(-0,5) - 2,4375 = - 0,8125 –2,4375 = -3,25,

Z(t*) < Z() (-3,25<-2,4375), то есть испытание удачное,

(S=S+0; S=1. S=1+0=1);

IV итерация.

1. Определяем координаты точки :

(0,75 - 1,5t; 0,5 - t). (0,75 - 1,5·(-0,5); 0,5 – (-0,5)).

(1,5; 1)

2. Проверим: принадлежит ли точка (1,5; 1) области допустимых решений?

2·1,5 + 1≤ 5? →4<5

1,5 + 3·1≤ 4? →4,5>4

1,5≥0; 1≥0

(1,5; 1) не принадлежит ОДР, т.е. испытание оказалось неудачным (S=S+1; S=1; S=1+1 S=2; S<M; 2<4).

Полагаем t*= t*/2 = - 0,5 / 2; t*= - 0,25, переходим к п. 7.

(0,75 - 1,5t; 0,5 - t). =(0,75 – 1,5×(-0,25); 0,5 + 0,25).

(0,75 + 0,375; 0,75); (1,125; 0,75).

Проверим: принадлежит ли точка (1,125; 0,75) ОДР?

2·1,125 + 0,75≤ 5? → 3 < 5

1,125 + 3·0,75≤ 4? →3,375 < 4

1,125≥0; 0,75≥0.

Точка (1,125; 0,75) Î ОДР.

Z()=(1,125)²+(0,75)² –3 × 1,125 - 2× 0,75 = 1,265625 + 0,5625 – 3,375 – 1,5 = = - 3,609375.

Z() < Z() (- 3,609375 < -2,4375), то есть испытание удачное, поэтому попрежнему S=2; S<M; 2<4.

Присваиваем () = (1,125; 0,75); Z() = Z() = - 3,609375.

На этом заканчивается IV итерация: (1,125; 0,75);

Z() = -3,609375.

Далее процесс повторяется с п. 3, нахождения grad Z() и т.д.