Графический метод

Задача называется задачей квадратичного программирования, если целевая функция содержит переменные во второй степени, а система ограничений - линейные выражения.

Пусть задача квадратичного программирования имеет две переменные X₁ и X₂.

Z(X₁,X₂)= C₁₁X₁²+C₁₂X₁X₂+C₂₂X₂²+C₁X₁+C₂X₂ +C₀

a_I1 X₁ +a_I2X₂.≤ a_{I 0} , i=1÷n, X₁≥0, X₂≥0

ОДР задач КП является либо выпуклый многоугольник, либо выпуклая неограниченная область с конечным числом вершин (как в линейном программировании). А линия уровня целевой квадратичной функции - кривая: либо окружность, либо эллипс, либо гипербола, либо парабола. Для всех линий уровня полагаем, что C₁₂=0, чтобы не делать преобразований целевой функции и не выполнять поворот осей.

1 случай. а) C₁₁=C₂₂>0.

Целевую функцию Z(X₁,X₂)= C₁₁X₁² +C₂₂X₂²+C₁X₁+C₂X₂ +C₀ приводим к виду Z(X₁,X₂)= C₁₁(X₁ -a)² +C₂₂ (X₂-b)²+C₀ . Линии уровня концентрические окружности с центром в точке O`(a,b).

б) C₁₁=C₂₂<0.

Целевую функцию Z(X₁,X₂)= C₁₁X₁² +C₂₂X₂²+C₁X₁+C₂X₂ +C₀ приводим к виду Z(X₁,X₂)= C₁₁(X₁-a)² +C₂₂ (X₂-b)²+C₀ . Линии уровня мнимые концентрические окружности с центром в точке O`(a,b).

2 случай. а) C₁₁ не равно C₂₂ и оба положительные; C₁₁·C₂₂>0.

Целевую функцию Z(X₁,X₂)= C₁₁X₁² +C₂₂X₂²+C₁X₁+C₂X₂ +C₀ приводим к виду Z(X₁,X₂)= C₁₁(X₁ -a)² +C₂₂ (X₂-b)²+C₀ . Линии уровня - подобные эллипсы с центром в точке O`(a,b).Отношение полуосей равно корню квадратному из отношения C₂₂ к C_11.

б) C₁₁ не равно C₂₂ и оба отрицательные; C₁₁·C₂₂ >0.

Целевую функцию Z(X₁,X₂)= C₁₁X₁² +C₂₂X₂²+C₁X₁+C₂X₂ +C₀ приводим к виду Z(X₁,X₂)= C₁₁(X₁ -a)² +C₂₂ (X₂-b)²+C₀ . Линии уровня мнимые подобные эллипсы с центром в точке O`(a,b). Отношение полуосей равно корню квадратному из отношения C₂₂ к C_11.

3 случай. C₁₁ не равно C_22, а C₁₁·C₂₂ < 0

Целевую функцию Z(X₁,X₂)= C₁₁X₁² +C₂₂X₂²+C₁X₁+C₂X₂ +C₀ приводим к виду Z(X₁,X₂)= C₁₁(X₁ -a)² +C₂₂ (X₂-b)²+C₀ . Линии уровня - подобные гиперболы с центром в точке O`(a,b). Асимптоты гипербол имеют вид: X₂ - b = K (X₁ -a) и X₂ - b = -K (X₁ -a). Коэффициент K равен корню квадратному из модуля отношения C₁₁ к C₂₂. Уравнения асимптот можно преобразовать к виду: X₂ = b + K (X₁ -a) и X₂ =b - K (X₁ -a).

4 случай. C₁₁·C₂₂ =0, причём одновременно C₁₁ и C₂₂ равняться нулю не могут. Линии уровня подобные параболы.

а) C₂₂ =0_, C₂ не равно нулю.

Целевую функцию Z(X₁,X₂)= C₁₁X₁² +C₁X₁+C₂X₂ +C₀ приводим к виду Z(X₁,X₂)= aX₁ ² +bX₁+c - X₂ . Линии уровня подобные параболы, ось симметрии которых параллельна оси ОX₂, а вершина имеет координаты (-b/2a; X₂).

б) C ₁₁ =0_, C₁ не равно нулю.

Целевую функцию Z(X₁,X₂)= C₂₂X₂² +C₂X₂+ C₁X₁ +C₀ приводим к виду Z(X₁,X₂)= aX₂ ² +bX₁+c - X₁ . Линии уровня подобные параболы, ось симметрии которых параллельна оси ОX₁, а вершина имеет координаты (X₁;-b/2a).

в) C₂= C₂₂ =0.

Целевую функцию Z(X₁,X₂)= C₁₁X₁² +C₁X₁+C₀ приводим к виду Z(X₁,X₂)= aX₁ ² +bX₁+c. Линии уровня прямые, параллельные оси ОX₂, если b²-4ac >0 и мнимое место точек, если b²-4ac <0

г) C₁=C₁₁=0.

Целевую функцию Z(X₁,X₂)= C₂₂X₂² +C₂X₂ +C₀ приводим к виду Z(X₁,X₂)= aX₂ ² +bX₂+c. Линии уровня прямые, параллельные оси ОX₁, если b²-4ac >0 и мнимое место точек, если b²-4ac <0.

Случай 1.

Пример 21.Найтиграфически максимум и минимум.

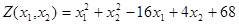
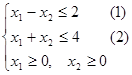
Решение.

1. Областью допустимых решений является четырехугольник ABCD (рис.10).

2. С₁₂ = 0, С₁₁ = С₂₂ =1. Следовательно, линиями уровня целевой функции являются концентрические окружности. Найдем их центр. Для этого сведем данную квадратичную функцию к каноническому виду.

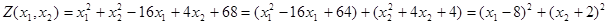3. Центром концентрических окружностей является точка О₁ (8;-2).

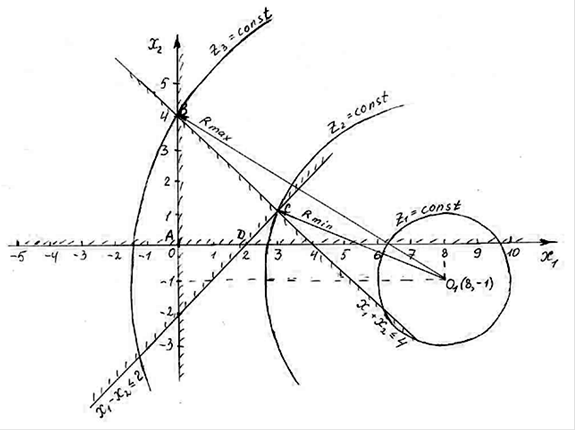
4. Минимальное значение целевой функции соответствует наименьшему радиусу и достигается в точке, в которой окружность в первый раз касается области допустимых решений, т.е. точке области допустимых решений, наименее удаленных от точки О₁. Это точка C(3;1).

min Z(C) = (x₁ -8)² + (x₂ +2)² =(3-8)² + (1+2)² = 34.

Максимальное значение целевой функции соответствует наибольшему радиусу и достигается в точке, в которой окружность последний раз касается области допустимых решений, т.е. точке области допустимых решений наиболее удаленной от точки О₁. Это точка В (0;4).

max Z(В) = (x₁ -8)² + (x₂ +2)² =(0-8)² + (4+2)² = 100.

Следовательно, min Z(3;1) =34, max Z(0;4) = 100.

Рис. 10. Целевая функция - концентрические окружности

Случай 2.

Если коэффициенты целевой функции С₁₂ = 0, С₁₁ ¹ С₂₂, С₁₁ · С₂₂ > 0, то квадратичную целевую функцию можно свести к каноническому виду Z(X₁,X₂)= C₁₁(X₁ -a)² +C₂₂ (X₂-b)². В этом случае линиями уровня являются подобные эллипсы с центром в точке О₁ (а, в) и отношением полуосей, равным .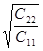

Пример 21.Найти графически максимум и минимум.

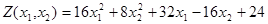
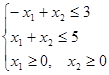
Преобразуем целевую функцию Z:

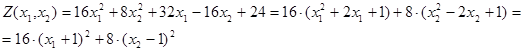
Линии уровня – концентрические эллипсы с центром в точке с координатами (–1;1).

Решение.

1. Областью допустимых решений является четырехугольник ABCD (рис. 11).

2. С₁₂ = 0, С₁₁ ¹ С₂₂, С₁₁> 0, С₂₂ > 0, С₁₁ · С₂₂ > 0. Следовательно, линиями уровня целевой функции являются подобные эллипсы. Найдем их центр, для этого сведем данную квадратичную функцию к каноническому виду:

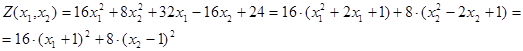
3. Центром подобных эллипсов является точка О₁(-1; 1). Отношение полуосей эллипсов равно .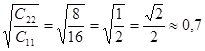

4. Минимальное значение целевой функции достигается в точке Е (0;1), в которой эллипс касается области допустимых решение ABCD.

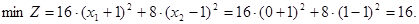
Максимальное значение целевой функции достигается в точке D(5; 0).

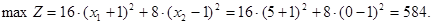
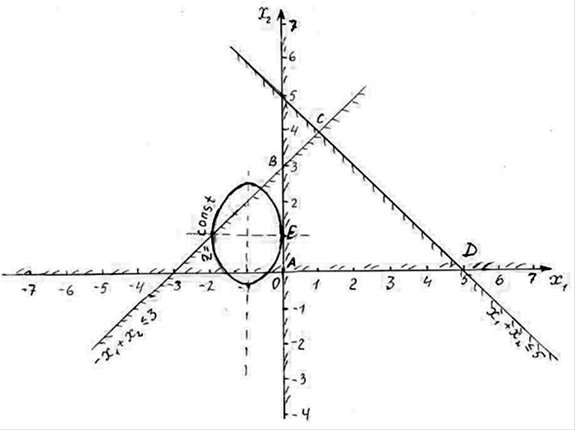
Рис. 11. Целевая функция – подобные эллипсы

Случай 3.

Если коэффициенты целевой функции С₁₂ =0, С₁₁·С₂₂< 0, то квадратичную целевую функцию можно свести к каноническому виду:

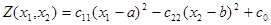
Пусть С₁₁> 0, С₂₂ < 0. В этом случае линиями уровня являются подобные гиперболы с центром в точке О₁ (а, в) и асимптотам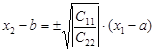и или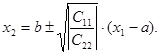

Пример 22. Найти графически максимум и минимум.

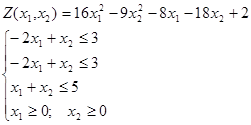
Решение.

1. Областью допустимых решений является четырехугольник ABCD (рис.12).

2. С₁₂ =0, С₁₁·С₂₂ =16·(-9) = -144 < 0. Следовательно, линиями уровня целевой функции являются подобные гиперболы. Найдем их центр, для этого сведем данную квадратичную функцию к каноническому виду:

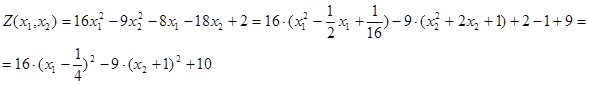3. Центром подобных гипербол является точка О₁(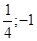). Уравнение асимптот: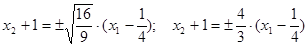

4. Строим гиперболы:

Первый способ.

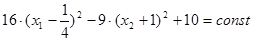
а) Положим const = 11, получим

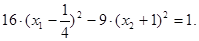Сделаем перенос начала координат в точку

О₁ (1/4; -1). Пусть 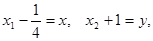тогда 16х² -9у² =1 или

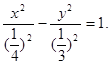
Вершинами гиперболы являются точки (-1/4; 0); (1/4; 0) в новой системе координат (ХО₁У). Осью симметрии является ось О₁Х.

б) Положим const = 154, получим

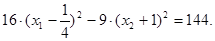Разделим обе части уравнения на 144, получим .

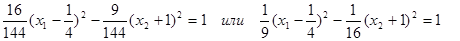Сделаем перенос начала координат в точку О₁(1/4; -1). Пусть 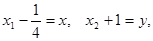тогда 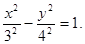Вершинами гиперболы являются точки (-3; 0) и (3; 0) в новой системе координат (ХО₁ У). Осью симметрии являются ось О₁Х.

в) Положим const = 9, получим 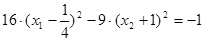или

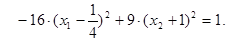Сделаем перенос начала координат в точку О₁(1/4; -1). Пусть 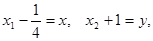тогда -16х² +9у² =1 или

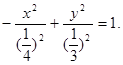
Вершины гиперболы – точки (0; -1/3); (0; 1/3) в новой системе координат (ХО₁ У). Осью симметрии являются ось О₁У.

г) Положим const = -134, получим 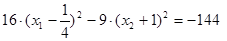или

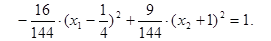Выполним сокращение, получим

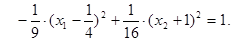Сделаем перенос начала координат в точку О₁(1/4; -1). Пусть 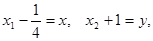тогда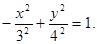

Вершинами гиперболы являются точки (0; -4); (0; 4) в новой системе координат (ХО₁ У). Осью симметрии являются ось О₁У.

д) Положим const = 10, получим 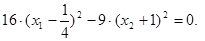Сделаем перенос начала координат в точку О₁(1/4; -1). Пусть 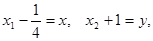тогда

16х² – 9у² = 0 или (4х – 3у) · (4х + 3у) = 0. Это уравнение распадается на два: (4х – 3у) = 0 и (4х + 3у) = 0. Откуда 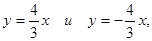а это уравнения асимптот в новой системе координат (ХО₁ У).

Второй способ.

Можно взять произвольную точку, подставить ее в целевую функцию, узнать значение Z и приближенно построить целевую функцию по отношению к асимптотам.

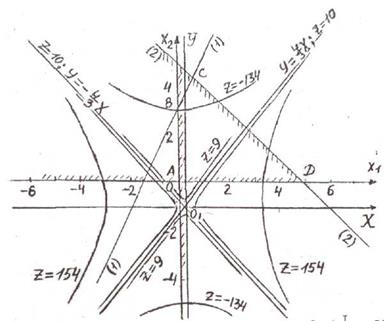
Рис.12. Целевая функция – подобные гиперболы

5. Минимальное значение целевой функции достигается в точке 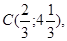в которой гипербола касается области допустимых решений АBCD.

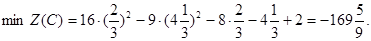
Максимальное значение целевой функции достигается в точке D(5; 0).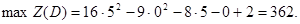

Случай 4.

Если коэффициенты целевой функции С₁₂ =0 и С₁₁ · С₂₂ = 0, причем одновременно С₁₁ и С₂₂ равняться нулю не могут, то квадратичную целевую функцию можно свести к каноническому виду: Z(X₁,X₂)= aX₁ ² +bX₁+c - X₂, если С₂ ¹ 0, а С₂₂ =0. В этом случае линиями уровня являются параболы, ось симметрии которых параллельна оси ОХ₂.

Пример 24.Найти графически максимум и минимум задачи квадратичного программирования.

Z(x₁, x₂) =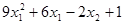

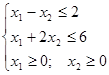
Решение.

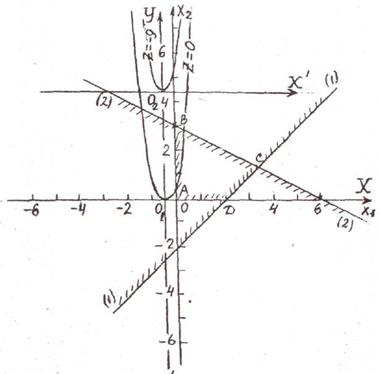
1. Областью допустимых решений является четырехугольник ABCD (рис. 13).

2. С₂ ¹ 0, С₂₂ =0, С₁₁ ¹ 0, следовательно, линиями уровня являются подобные параболы, ось симметрии которых параллельна оси ОХ₂.

3. Найдем каноническое уравнение параболы:

.

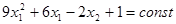Положим const = 0, тогда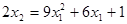

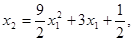то есть получим X₂ =aX₁ ² +bX₁+c.

4. Найдем вершину параболы:

Х₀ = 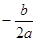или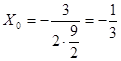

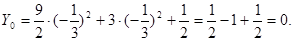
5. Сделаем перенос начала координат в точку О₁ (Х₀, У₀), О₁ (-1/3; 0).

6. В новых координатах (Х’О₁У) уравнение параболы имеет вид у=ах² или у= .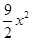

7. Положим const = - 9, тогда . .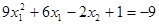

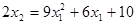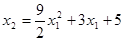, то есть получили X₂ =aX₁ ² +bX₁+c.

Рис.13. Целевая функция – подобные параболы

8. Найдем вершину параболы:

.

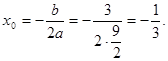
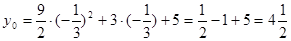9. Сделаем перенос начала координат в точку О₂(х₀, у₀), О₂ .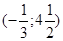

10. В новых координатах (Х’О₁У) уравнение параболы имеет вид у=ах² или у= .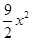

11. Минимальное значение целевой функции достигается в точке B(0;3). min Z = 9·0² +6·0 - 2·3 + 1 = - 5.

Максимальное значение целевой функции достигается в точке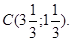

.

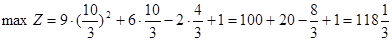Замечание. Если в выражении 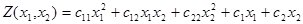коэффициент с₁₂ ¹0, то кроме переноса начала координат, необходимо повернуть координатные оси на такой угол, чтобы исчез член с произведением переменных.

Контрольные вопросы

1. Какая функция называется выпуклой?

2. Какая функция называется гладкой?

3. Какая функция называется квадратичной?

4. Какая функция имеет локальный максимум, а какая - абсолютный?

5. В чем разница между локальным и абсолютным максимумом?

6. Какие методы поиска Вы знаете?

7. Какой вид линии уровня задач квадратичного программирования Вы знаете?

8. Всегда ли задача квадратичного программирования имеет решение?