Нелинейное программирование. Методы спуска. Приближенное решение задач нелинейного программирования градиентным методом.
Общая задача мат. программирования формулируется: найти вектор
X = (x 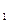 ………..x
………..x 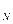 ), удовлетворяющий системе ограничений
), удовлетворяющий системе ограничений
g 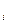 (x
(x 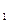 ………..x
………..x 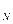 ) = b
) = b  i=1,2,…,k
i=1,2,…,k
g 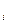 (x
(x 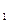 ………..x
………..x 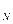 )
) 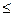 b
b  i=k+1,k+2,…,m
i=k+1,k+2,…,m
и доставляющий экстремум функции
Z = f (x 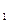 ………..x
………..x 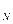 ).
).
При этом предполагается, что известны функции g  (x
(x 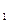 ………..x
………..x 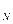 ) и f (x
) и f (x 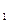 ………..x
………..x 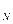 ). Обычно на некоторые переменные x
). Обычно на некоторые переменные x 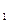 ………..x
………..x 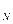 накладывается условие неотрицательности. Кроме того, ограничением может служить условие целочисленности решения для ряда переменных. Если g
накладывается условие неотрицательности. Кроме того, ограничением может служить условие целочисленности решения для ряда переменных. Если g  (x
(x  ………..x
………..x 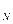 ) =
) = 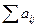 x
x 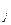 и Z = f (x
и Z = f (x 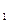 ………..x
………..x 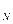 ) =
) = 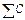
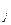 X
X 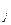 ., где
., где
a 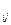 и C
и C 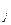 известные константы, то при условие неотрицательности решения получаем задачу линейного программирования. Любую другую задачу мат. программирования будем считать нелинейной.
известные константы, то при условие неотрицательности решения получаем задачу линейного программирования. Любую другую задачу мат. программирования будем считать нелинейной.
Методы спуска. Градиентный метод наискорейшего спуска.
Z=f(x1,…xn) 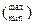
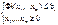
строится последовательность точек
x0,x1,…xn, каждая является решением системы ограничений
при этом переход от одной точки к другой:
xi+1=xi+λ 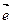 ,
, 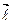 =(
=(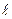 1,
1, 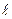 2,…
2,… 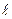 n)-вектор, задающий направление
n)-вектор, задающий направление
λ-шаг итерации
λ и 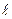 выбирается таким образом, что бы обеспечить сходимость х0,…хn к соответствующей точке оптимума
выбирается таким образом, что бы обеспечить сходимость х0,…хn к соответствующей точке оптимума
хк+1=(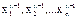 )
)
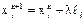 , i=1,…n
, i=1,…n
Если последовательность бесконечна, то с определенной степенью точности можно выбрать Хк0 
 2015-07-04
2015-07-04 287
287







