Задачи-оценки, как правило, более сложны. Но и решать их интереснее. Сначала нужно как можно точнее и при этом наиболее проще описать процесс, явление, обсуждаемое в задаче. Стараться не упустить главное, выбрасывая второстепенные детали. Далее необходимо вспомнить физические законы, уместные в данном случае. Затем применить адекватное математическое описание проблемы. После соответствующих преобразований получить ответ в наиболее простом аналитическом виде. Часто здесь помогают «соображения размерности». Например, если оценивается величина силы, то из влияющих параметров задачи (например, массы, скорости т.д.) необходимо сконструировать выражение с размерностью ньютон. Численные значения влияющих на ответ факторов взять из своего опыта и опыта товарищей. Например, сила, которую может развивать студент ФЕН, по порядку величины близка к его весу. Как известно, все студенты одинаковы и имеют массу 80 кг. Полученную в результате решения задачи-оценки величину сравнить с личными ощущениями. Для этого мысленно встроить себя в задачу и постараться почувствовать все на себе.
19. Оценить силу давления вертикального дождя на развернутый зонт стоящего студента ФЕН.
Решение:
Капли дождя при падении на зонт останавливаются. Импульс капель меняется, изменение импульса капель равно импульсу силы, действующей на них со стороны зонта. Соответственно, со стороны капель на зонт действует такая же, но противоположно направленная сила. Вспомним альтернативную запись второго закона Ньютона 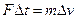 , тогда сила, действующая на зонтик студента ФЕН, равна изменению импульса капель дождя, выпадаемых на зонтик в единицу времени.
, тогда сила, действующая на зонтик студента ФЕН, равна изменению импульса капель дождя, выпадаемых на зонтик в единицу времени.
Оценим массу воды, которая попадает на зонт за 1 с. Исходя из нормы выпадения осадков (300-500 мм в год для Новосибирска), времени, которое идет средний дождь, и примерного размера зонта 1 м2, получаем, что на зонт попадает 10 г воды в секунду.
Полезно при случае поставить открытую банку с водой под дождь, измерить поток воды и оценить, сколько воды было в туче до дождя. Сколько потенциальной энергии пропадает зря!
Положим, что скорость капель воды перед падением на зонт 10 м/с.
Подставив в соотношение
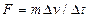
оценочные значения
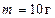
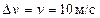
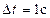
получим, что сила давления на зонт примерно равна 0,1 Н.
20. Может ли студент ФЕН сдвинуть или перевернуть тяжелый кубик из платины, лежащий на столе? Ребро куба 10 см.
Решение:
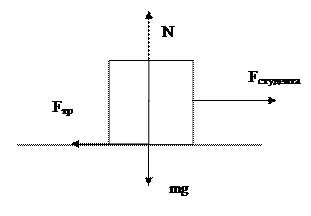 Рассмотрим случай, когда кубик не переворачивается. Тогда сила, с которой действует студент, должно быть больше силы трения, возникающей между опорой и кубиком из платины:
Рассмотрим случай, когда кубик не переворачивается. Тогда сила, с которой действует студент, должно быть больше силы трения, возникающей между опорой и кубиком из платины: 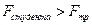 . Силу трения оценим исходя из
. Силу трения оценим исходя из 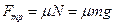 .
.
Массу кубика легко оценить, если вспомнить, что платина имеет высокую плотность. Даже если точная цифра не вспомнится, то примерно посчитаем, что плотность платины 20 г/см3. Тогда масса кубика 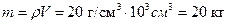 . То есть примерно как два больших ведра с водой. Если положить, что коэффициент трения скольжения металла по деревянной поверхности около 0,5, то для сдвига кубика необходимо развить силу
. То есть примерно как два больших ведра с водой. Если положить, что коэффициент трения скольжения металла по деревянной поверхности около 0,5, то для сдвига кубика необходимо развить силу 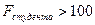 ньютон. Нормальный человек развивает силу по порядку величины равную своему весу. При массе тела 80 кг это 800 ньютон. Отсюда понятно, что любой студент ФЕН может сдвинуть кубик из платины.
ньютон. Нормальный человек развивает силу по порядку величины равную своему весу. При массе тела 80 кг это 800 ньютон. Отсюда понятно, что любой студент ФЕН может сдвинуть кубик из платины.
Из сравнения моментов сил видно, для переворачивания кубика может потребоваться вдвое меньшая сила, чем для сдвига. Однако при коэффициенте трения меньше 0,5 кубик перевернуть нельзя, можно только сдвинуть.
 2015-07-04
2015-07-04 1278
1278








