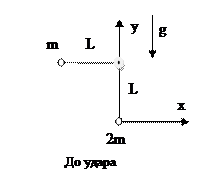
В гравитационном поле g на тонких нитях длины L каждая, закрепленных в одной точке, висят два одинаковых по размеру шара радиуса R<<L и массы m и 2m. Легкий шар отклоняют до горизонтального положения нити и отпускают. Найти, на какие максимальные углы отклонятся шары после первого удара. До удара тяжелый шар покоится. Найти ускорения тел (модуль и направление) сразу же после отпускания легкого тела и сразу же после удара. Найти натяжения нитей в указанные моменты времени. Трения нет, удар абсолютно упругий.
Решение:
1) Пусть 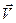 - скорость легкого шара до момента удара,
- скорость легкого шара до момента удара, 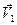 - скорость легкого шара после удара,
- скорость легкого шара после удара, 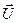 - скорость тяжелого шара после удара.
- скорость тяжелого шара после удара.
2) Потенциальная энергия легкого шара переходит в его кинетическую энергию перед столкновением. С учетом выбранной системы координат имеем: 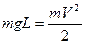 , откуда
, откуда 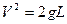 .
.

3) Кинетическая энергия легкого шара перед ударом переходит в кинетическую энергию легкого и тяжелого шара сразу после удара: 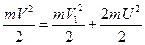 или
или 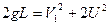 . Кроме этого, суммарный импульс шаров до взаимодействия равен суммарному импульсу после взаимодействия:
. Кроме этого, суммарный импульс шаров до взаимодействия равен суммарному импульсу после взаимодействия: 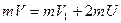 или
или 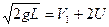 . Т.о. имеем систему:
. Т.о. имеем систему:
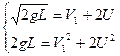
Решая данную систему, получаем: 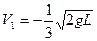 (легкий шар отскакивает от тяжелого в обратную сторону).
(легкий шар отскакивает от тяжелого в обратную сторону). 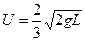
4) После взаимодействия кинетическая энергия шаров переходит в потенциальную:
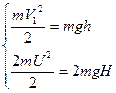
или с учетом 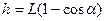 и
и 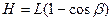 , получаем соотношения:
, получаем соотношения:
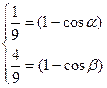 ,
,
откуда 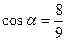 ,
, 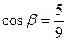 .
.
5) Сразу после отпускания легкого шара его скорость равна нулю, натяжение нити будет нулевым (см. рисунок до удара), поэтому ускорение будет равно ускорению свободного падения - 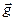 .
.
6) Сразу после удара результирующие ускорения буду направлены к точке подвеса и равны: 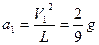 - для легкого шара,
- для легкого шара, 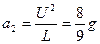 - для тяжелого шара. Поскольку длина нити много больше радиусов шаров, то можно считать, что все силы направлены вдоль оси
- для тяжелого шара. Поскольку длина нити много больше радиусов шаров, то можно считать, что все силы направлены вдоль оси 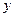 . В этом случае, натяжения нитей сразу после удара можно найти из соотношения сил:
. В этом случае, натяжения нитей сразу после удара можно найти из соотношения сил:
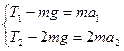 или
или 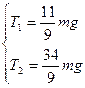
Ответ: 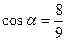 ,
, 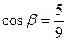 ; после отпускания легкого шара его ускорение равно
; после отпускания легкого шара его ускорение равно 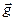 ; после удара
; после удара 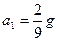 ,
, 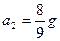 ,
, 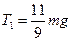 ,
, 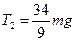 .
.
 2015-07-04
2015-07-04 473
473








