Свойства постоянной функции

· Область определения: все множество действительных чисел.

· Постоянная функция является четной.

· Область значений: множество, состоящее из единственного числа С.

· Постоянная функция невозрастающая и неубывающая (на то она и постоянная).

· Говорить о выпуклости и вогнутости постоянной не имеет смысла.

· Асимптот нет.

· Функция проходит через точку (0,C) координатной плоскости.

Корень n -ой степени.

Рассмотрим основную элементарную функцию, которая задается формулой 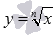, где n – натуральное число, большее единицы.

Корень n -ой степени, n - четное число.

Начнем с функции корень n -ой степени при четных значениях показателя корня n.

Для примера приведем рисунок с изображениями графиков функций 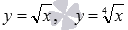и 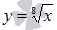, им соответствуют черная, красная и синяя линии.

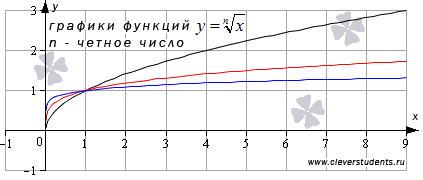
Аналогичный вид имеют графики функций корень четной степени при других значениях показателя.

Свойства функции корень n -ой степени при четных n.

· Область определения: множество всех неотрицательных действительных чисел .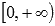

· При x=0 функция 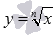принимает значение, равное нулю.

· Эта функция общего вида (не является четной или нечетной).

· Область значений функции: .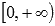

· Функция 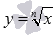при четных показателях корня возрастает на всей области определения.

· Эта функция имеет выпуклость, направленную вверх, на всей области определения, точек перегиба нет.

· Асимптот нет.

· График функции корень n -ой степени при четных n проходит через точки (0,0) и (1,1).

Корень n -ой степени, n - нечетное число.

Функция корень n -ой степени с нечетным показателем корня n определена на всем множестве действительных чисел. Для примера приведем графики функци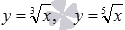й и 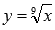, им соответствуют черная, красная и синяя кривые.

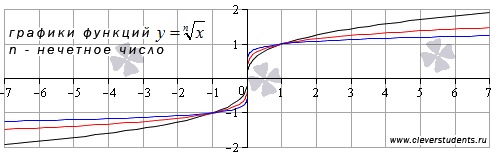
При других нечетных значениях показателя корня графики функции 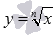будут иметь схожий вид.

Свойства функции корень n -ой степени при нечетных n.

· Область определения: множество всех действительных чисел.

· Эта функция нечетная.

· Область значений функции: множество всех действительных чисел.

· Функция 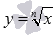при нечетных показателях корня возрастает на всей области определения.

· Эта функция вогнутая на промежутке 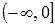и выпуклая на промежутке 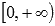, точка с координатами (0,0) – точка перегиба.

· Асимптот нет.

· График функции корень n -ой степени при нечетных n проходит через точки (-1,-1), (0,0) и (1,1).