Нелинейная регрессия

При изучении зависимости экономических показателей на основе реальных статистических данных с использованием аппарата теории вероятностей и математической статистики можно сделать выводы, что линейные зависимости встречаются не так часто. Их используют как частный случай для удобства и наглядности рассмотрения протекаемого экономического процесса. Чаще встречаются модели, которые отражают экономические процессы в виде нелинейной зависимости. Например, затухающие гармонические (или негармонические) колебания с экономической точки зрения могут характеризовать объемы продаж сезонного товара на этапе ухода с рынка. Зависимость в виде выпуклой параболы может характеризовать жизненный цикл товара, а график в виде вогнутой параболы - ремаркетинг. Существует еще так называемая кусочная функция, которая на разных участках области определения может быть задана разными аналитическими выражениями. Один из самых простых ее видов – кусочно-линейная функция, в которой каждая входящая кусочная функция является линейной (зигзаг из прямых линий). Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций.

Различают два класса нелинейных регрессий:

1) нелинейные относительно объясняющих переменных, но линейные по оцениваемым параметрам;

2) нелинейные по оцениваемым параметрам.

Класс регрессий, нелинейных по объясняющим переменным, но линейных по оцениваемым параметрам, включает уравнения, в которых зависимая переменная линейно связана с параметрами. Примеры таких регрессий:

· полиномы разных степеней 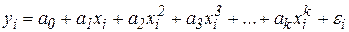(полином k -ой степени);

· равносторонняя гипербола .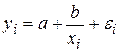

При оценке параметров регрессий, нелинейных по объясняющим переменным, используется метод замены переменных. Суть его состоит в замене нелинейных объясняющих переменных новыми линейными переменными, в результате чего нелинейная регрессия сводится к линейной. К новой, преобразованной регрессии может быть применен обычный МНК.

Пример. Дано:

Температура Х, °С
Объем выпуска продукции Y, шт.

Построить модель зависимости объема выпускаемой продукции от температуры при технологическом процессе с помощью полинома второй степени (парабола второй степени): 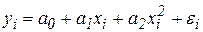. Исходные данные и результаты расчетов отобразить на графике.

Решение (сделайте самостоятельно по задаче из 1 семестра). Введем новую переменную 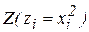, получим двухфакторное уравнение линейной регрессии: 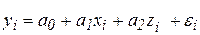, для оценки параметров которого используем обычный МНК. В результате получают модель .

Полином любого порядка сводится к линейной регрессии с ее методами оценивания параметров и проверки гипотез. Среди нелинейной полиноминальной регрессии чаще всего используется парабола второй степени; в отдельных случаях – полином третьего порядка. Ограничение в использовании полиномов более высоких порядков связано с требованием однородности исследуемой совокупности: чем выше порядок полинома, тем больше изгибов имеет кривая и, соответственно, менее однородна совокупность по результативному признаку.

Равносторонняя гипербола, для оценки параметров которой применяется тот же метод замены переменных (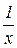 заменяют на переменную z) может быть использована для характеристики связи удельных расходов сырья, материалов и топлива с объемом выпускаемой продукции. Построить: 1) диаграмму рассеяния; 2) модель регрессии зависимости темпов инфляции от нормы безработицы. Результаты расчетов отобразить на графике.

Пример. Дано:

Темпы инфляции Y	1,1	1,1	1,2	1,3	1,7	2,9	2,9	4,2	5,4
Норма безработицы Х	6,5	5,4	5,5	5,0	4,4	3,7	3,7	3,5	3,4

Решение. 1. Построить диаграмму рассеяния для переменной Х (процент безработных в общей численности рабочей силы) и Y (темпы инфляции) по данным табл. Характер диаграммы рассеяния явно указывает на наличие нелинейной связи между рассматриваемыми переменными. Если подобрать МНК линейную зависимость 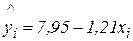, то она очевидным образом не соответствует характеру статистических данных, хотя значение коэффициента детерминации 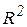=0,7184 и представляется достаточно высоким. В связи с этим при подборе моделей к реальным статистическим данным следует обращать внимание не только на коэффициент детерминации, но и обязательно на соответствие подобранной модели характеру статистических данных. Здесь рассматривается модель равносторонней гиперболы 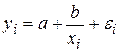, соответствующую линейной связи между переменными Y и Z: 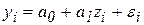, где 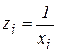. Подбор такой связи приводит к модели 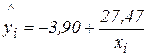с достаточно высоким коэффициентом детерминации 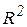=0,8307.

На практике подбор наилучшей модели регрессии выполняют с помощью специальных программных продуктов: Statistica, SSPS, VSTAT, СТАТЭКСПЕРТ и т.п. Использование ППП СТАТЭКСПЕРТ позволило получить модель 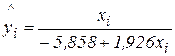с еще большим коэффициентом детерминации 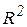=0,985.

К классу регрессий, нелинейных по оцениваемым параметрам, относятся уравнения, в которых зависимая переменная нелинейно связана с параметрами:

· степенная ;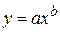

· показательная ;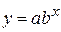

· экспоненциальная .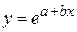

Если нелинейная модель внутренне линейна, то она с помощью соответствующих преобразований может быть приведена к линейному виду, например, логарифмированием и заменой переменных. Если же нелинейная модель внутренне нелинейна, то она не может быть сведена к линейной функции и для оценки ее параметров используются итеративные процедуры, успешность которых зависит от вида уравнений и особенностей применяемого итеративного подхода.

Примером регрессии, нелинейной по параметрам, но внутренне линейной, является степенная функция, которая широко используется в экономических исследованиях при изучении зависимости спроса от цен: 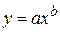, где 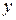- величина спроса; х – цена товара. Данная модель нелинейна относительно оцениваемых параметров, так как включает параметры a и b неаддитивно. Однако ее можно считать внутренне линейной, ибо логарифмирование данного уравнения по основанию е приводит его к линейному виду: 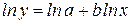. Заменив переменные и параметры, получим линейную регрессию, оценки параметров которой a и b могут быть найдены с помощью МНК. Широкое использование функции 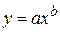связано тем, что параметр b в ней имеет четкое экономическое истолкование - он является коэффициентом эластичности. Это значит, что величина коэффициента b показывает, на сколько процентов изменится в среднем результат, если фактор изменится на 1%. Коэффициент эластичности можно определить и при других формах связи, но только для степенной функции он представляет собой постоянную величину, равную параметру b.

Пример. По 12-ти областям получена информация, характеризующая зависимость потребительских расходов Y на душу населения от денежных доходов X:

№ области	Расходы Y, руб.	Доходы Х, руб.	№ области	Расходы Y, руб.	Доходы Х, руб.

1) Построить степенную модель. 2) Оценить модель, определив индекс корреляции, среднюю относительную ошибку и коэффициент детерминации. 3) Исходные данные и результаты расчетов изобразить на графике.

Решение. Уравнение степенной модели: 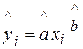. Для построения этой модели необходимо произвести линеаризацию переменных. Для этого прологарифмируем обе части уравнения: 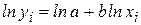. Обозначим YL = lnY = 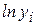; XL=lnX= 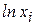; AL=lna. Тогда уравнение примет вид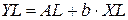 - линейного уравнения регрессия. Для оценки этого уравнения используется обычный МНК. Полученное уравнение регрессии имеет вид: .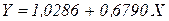

Затем, возвращаются к исходным переменным Х и Y, выполнив потенцирование данного уравнения: 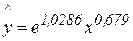( 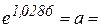2,797). Получим уравнение степенной модели регрессии: .

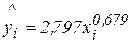	№ области	Расходы Y, руб.	Доходы Х, руб.	YL	XL	y^=2,797xi0,679	(yi-y^)2	(yi-ycp)2
				5,2983	6,3279	205,4528	29,7334	9587,6736
				5,3936	6,4297	220,1539	0,0237	6071,0069
				5,4381	6,4922	229,7010	0,0894	4612,6736
				5,4806	6,5367	236,7396	10,6299	3354,3403
				5,5413	6,6333	252,7929	4,8712	1841,8403
				5,6348	6,7799	279,2519	0,5596	321,0069
				5,7366	6,9078	304,5737	29,4442	146,0069
				5,7991	7,0031	324,9362	25,6421	1029,3403
				5,8861	7,1701	363,9653	15,7238	3854,3403
				5,9135	7,2079	373,4127	11,6466	5196,0069
				5,9402	7,2442	382,7484	7,5538	6737,6736
				5,9915	7,3132	401,1053	1,2218	10421,0069
Сумма				68,0536	82,0461	3574,8339	137,1394	53172,9167
Среднее		297,9167	985,00	5,6711	6,8372	297,9028	11,4283	4431,0764

2. Определяем индекс корреляции:

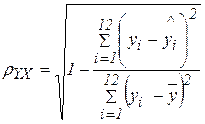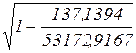= =0,9987. Связь между показателем Y и фактором Х можно считать достаточно сильной. Коэффициент детерминации 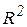= =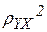0,9974. Вариация результата Y на 99,74% объясняется вариацией фактора Х.

	Расходы Y, руб.	Доходы Х, руб.	y^=2,797xi0,679	(yi-ycp)2	ei		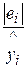еi2
			205,4636	9587,6736	-5,4636	0,0266	29,8513
			220,1655	6071,0069	-0,1655	0,0008	0,0274
			229,7130	4612,6736	0,2870	0,0012	0,0823
			236,7521	3354,3403	3,2479	0,0137	10,5489
			252,8062	1841,8403	2,1938	0,0087	4,8127
			279,2666	321,0069	0,7334	0,0026	0,5378
			304,5898	146,0069	5,4102	0,0178	29,2707
			324,9533	1029,3403	5,0467	0,0155	25,4693
			363,9845	3854,3403	-3,9845	0,0109	15,8759
			373,4323	5196,0069	-3,4323	0,0092	11,7810
			382,7685	6737,6736	-2,7685	0,0072	7,6648
			401,1264	10421,0069	-1,1264	0,0028	1,2688
Сумма			3575,0219	53172,9167	-0,0219	0,1171	137,1910

Средняя относительная ошибка 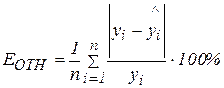= =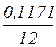0,009757272%»1%. В среднем расчетные значения 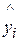для степенной модели отличаются от фактических значений на 1%.

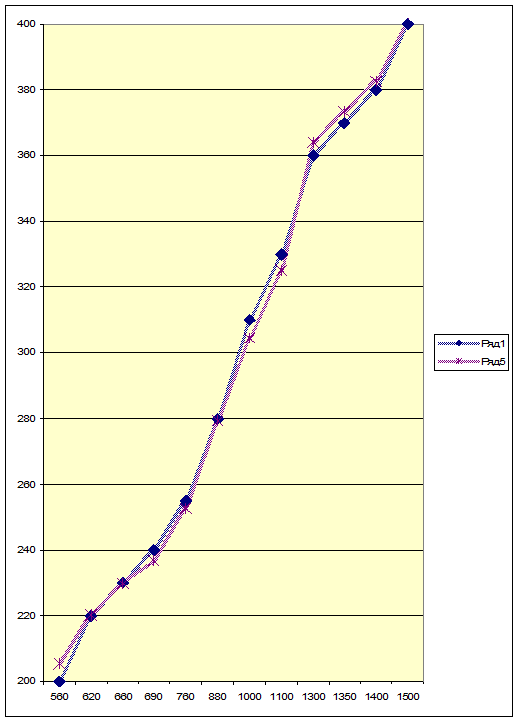
На рис. изображены исходные данные и результаты моделирования.