Пусть требуется приближенно решить уравнение 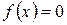 .
.
Эта задача может быть решена точно лишь для очень узкого класса функций. Уже для многочленов степени выше четырех не существует формул, выражающих их корни через коэффициенты с помощью радикалов. Для большинства же уравнений, встречающихся в различных приложениях математики и технических задачах, приближенные методы решения являются единственно возможными.
Приближенное решение уравнения распадается на несколько задач:
1) Локализация и отделение корня.
2) Вычисление корня уравнения с заданной точностью 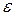 .
.
Локализация корней ¾ необходимо определить количество, характер и расположение корней на числовой прямой. Все следующие задачи решаются для каждого корня в отдельности. Отделение корня ¾ нужно указать отрезок 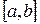 , внутри которого лежит один и только один корень данного уравнения. Локализация и отделение корня обычно выполняется графически и опирается на теорему: Если непрерывная функция
, внутри которого лежит один и только один корень данного уравнения. Локализация и отделение корня обычно выполняется графически и опирается на теорему: Если непрерывная функция 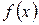 на концах отрезка
на концах отрезка 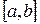 принимает значения разных знаков
принимает значения разных знаков 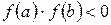 ,а первая производная постоянна по знаку, то на этом отрезке существует ровно одна точка, в которой функция обращается в ноль.
,а первая производная постоянна по знаку, то на этом отрезке существует ровно одна точка, в которой функция обращается в ноль.
Вычислить корень 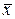 с заданной точностью
с заданной точностью 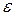 значит подобрать такое число
значит подобрать такое число 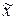 , для которого выполняется неравенство
, для которого выполняется неравенство 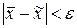 , то есть указать на числовой прямой точку, лежащую на расстоянии не большем, чем допустимая погрешность, от точного значения корня. Вычисление корня уравнения с заданной точностью
, то есть указать на числовой прямой точку, лежащую на расстоянии не большем, чем допустимая погрешность, от точного значения корня. Вычисление корня уравнения с заданной точностью 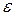 может быть выполнено различными методами [2].
может быть выполнено различными методами [2].
Метод половинного деления. Отрезок 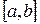 , содержащий корень уравнения, делим пополам точкой
, содержащий корень уравнения, делим пополам точкой 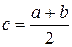 . Если
. Если 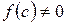 , из двух получившихся отрезков
, из двух получившихся отрезков 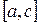 и
и 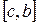 выбираем тот, который содержит корень уравнения. То есть тот отрезок на концах которого, функция принимает значения разных знаков. Этот новый отрезок
выбираем тот, который содержит корень уравнения. То есть тот отрезок на концах которого, функция принимает значения разных знаков. Этот новый отрезок 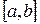 делим пополам и т.д. Процесс деления продолжается до тех пор, пока длина отрезка
делим пополам и т.д. Процесс деления продолжается до тех пор, пока длина отрезка 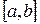 не станем меньше
не станем меньше 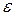 , тогда в качестве
, тогда в качестве 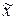 можно взять любую точку отрезка
можно взять любую точку отрезка 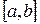 (Почему?).
(Почему?).
Метод касательных или метод Ньютона. Этот метод может быть использован только в том случае, если функция на отрезке не имеет точек перегиба, т.е. вторая производная постоянна по знаку. Тогда приближенное значение корня вычисляется по формуле 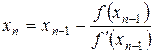 , где
, где 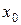 выбирается из условия
выбирается из условия 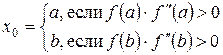 . Правило остановки вычислений для метода следующее: пусть
. Правило остановки вычислений для метода следующее: пусть 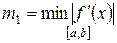 , тогда, если при некотором n выполняется
, тогда, если при некотором n выполняется 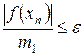 , можно положить
, можно положить 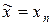 с погрешностью, не превышающей
с погрешностью, не превышающей 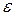 . Заметим, что данный метод отличается быстрой сходимостью.
. Заметим, что данный метод отличается быстрой сходимостью.
Метод итераций. Для применения этого метода уравнение 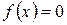 необходимо записать в виде
необходимо записать в виде 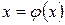 , причем
, причем 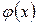 ¾сжимающая функция (
¾сжимающая функция (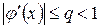 ). Приведем теорему, на которой основан универсальный способ преобразования исходного уравнения: Пусть
). Приведем теорему, на которой основан универсальный способ преобразования исходного уравнения: Пусть 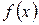 непрерывно дифференцируема на отрезке
непрерывно дифференцируема на отрезке 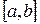 , причем
, причем 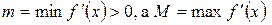 , тогда для любого
, тогда для любого 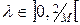 функция
функция 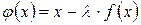 является сжимающей на отрезке
является сжимающей на отрезке 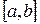 , причем при
, причем при 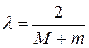 коэффициент сжатия принимает минимально возможное значение
коэффициент сжатия принимает минимально возможное значение 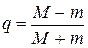 .
.
Выбрав произвольную точку 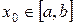 , последовательные приближения будем вычислять по формуле
, последовательные приближения будем вычислять по формуле 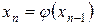 до тех пор, пока не будет выполнено условие
до тех пор, пока не будет выполнено условие 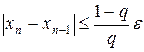 . Тогда
. Тогда 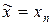 с погрешностью, не превосходящей
с погрешностью, не превосходящей 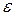 .
.
 2015-07-04
2015-07-04 346
346








