1. Для локализации и отделения корней построить график функции 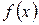 .. В результате для каждого корня должен быть получен отрезок
.. В результате для каждого корня должен быть получен отрезок 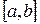 , содержащий только один корень уравнения.
, содержащий только один корень уравнения.
2. Вычислить корень, используя метод половинного деления. Результаты вычислений оформить в виде таблицы:
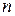
| 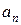
| 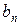
| 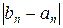
|
3. Вычислить корень методом Ньютона. Предварительно проверить выполнение условия применения, выбрать начальное приближение 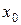 , найти значение
, найти значение 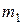 . Результаты расчетов внести в таблицу
. Результаты расчетов внести в таблицу
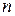
| 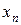
| 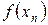
| 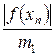
|
4. Вычислить корень методом итераций. Предварительно найти значения величин 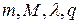 , записать уравнение в виде
, записать уравнение в виде 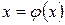 , выполнить расчеты. Для расчетов можно использовать систему MathCAD [6]. Результаты оформить в виде таблицы:
, выполнить расчеты. Для расчетов можно использовать систему MathCAD [6]. Результаты оформить в виде таблицы:
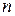
| 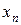
| 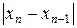
|
5. В полученных результатах сделать необходимые округления и записать в виде 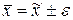 .
.
6. Сравнить методы приближенного решения уравнений.
Задание 1. Проанализировать решение кубического уравнения
Решим кубическое уравнение 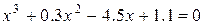 с абсолютной погрешностью
с абсолютной погрешностью 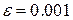 .
.
Запишем функцию и ее производные:
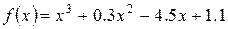 ,
, 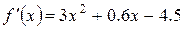 ,
, 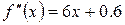 .
.
Вычислим корни первой и второй производной. 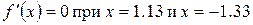 .
. 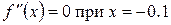 .
.
Из графика функции (Приложение 2) видно, что корни уравнения принадлежат отрезкам 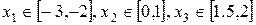 соответственно.
соответственно.
Корень 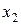 вычислим методом половинного деления. Вычисления оформим в виде таблицы (Таблица 1).
вычислим методом половинного деления. Вычисления оформим в виде таблицы (Таблица 1).
Таблица 1
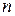
| 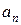
| 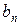
| 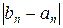
|
| 0.5 | 0.5 | ||
| 0.25 | 0.5 | 0.25 | |
| 0.25 | 0.375 | 0.125 | |
| 0.25 | 0.3125 | 0.0625 | |
| 0.25 | 0.28125 | 0.03125 | |
| 0.25 | 0.26563 | 0.01563 | |
| 0.25 | 0.25781 | 0.00781 | |
| 0.25 | 0.25391 | 0.00391 | |
| 0.25196 | 0.25391 | 0.00195 | |
| 0.25196 | 0.25293 | 0.00097 |
Вычисления можно прекратить, поскольку длина последнего отрезка не превосходит 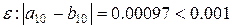 .
.
В качестве приближенного значения корня возьмем середину последнего отрезка 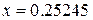 .
.
Методом Ньютона будем вычислять 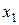 . Отрезок
. Отрезок 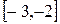 не содержит точек перегиба, т. к. вторая производная на нем постоянна по знаку. В качестве начального приближения возьмем
не содержит точек перегиба, т. к. вторая производная на нем постоянна по знаку. В качестве начального приближения возьмем 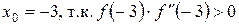 . Поскольку первая производная монотонна на данном отрезке (Почему?), ее минимум достигается на одном из концов отрезка. Поэтому возьмем
. Поскольку первая производная монотонна на данном отрезке (Почему?), ее минимум достигается на одном из концов отрезка. Поэтому возьмем 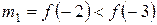 .
.
Результаты расчетов по методу Ньютона (Приложение 3) представим в таблице (Таблица 2).
Таблица 2
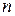
| 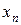
| 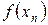
| 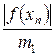
|
| -3 | -9.7 | 1.5398 | |
| -2.5314 | -1.8075 | 0.2869 | |
| -2.39452 | -0.1341 | 0.0213 | |
| -2.38262 | -9.74×10-4 | 1.55×10-4 |
Поскольку 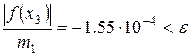 вычисления можно прекратить.
вычисления можно прекратить.
Последний корень вычислим методом итераций. Поскольку первая производная функции монотонна на отрезке 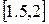 (Почему?) максимум и минимум достигается ею на концах отрезка, поэтому имеем
(Почему?) максимум и минимум достигается ею на концах отрезка, поэтому имеем 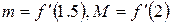 . Вычислим
. Вычислим 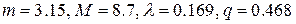 . Вычисления по методу итераций (Приложение 4) запишем в виде таблицы (Таблица 3).
. Вычисления по методу итераций (Приложение 4) запишем в виде таблицы (Таблица 3).
Таблица 3
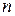
| 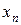
| 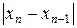
|
| 1.5 | ||
| 1.77004 | 0.27004 | |
| 1.83412 | 0.06408 | |
| 1.82979 | 4.32×10-3 | |
| 1.83034 | 5.42×10-4 |
На последнем шаге имеем 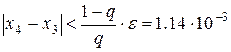 , вычисления можно прекратить.
, вычисления можно прекратить.
Сделаем необходимые округления и окончательно запишем 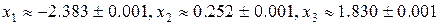
 2015-07-04
2015-07-04 364
364








