Решение

Вариант №3.

Задание 1. Найти неопределенный интеграл .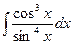

Задание 2. Найти площадь фигуры, ограниченной линиями .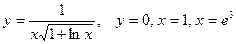

Задание 3. Вычислить несобственный интеграл 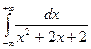или доказать его расходимость.

Задание 4. Найти направление, в котором функция 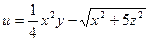возрастает в точке 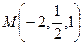быстрее всего.

Задание 5. Найти экстремум функции 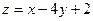при условии, что её аргументы удовлетворяют уравнению .

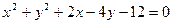Задание 6. Вычислить 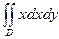, где область D ограничена линиями .

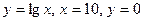Задание 7. Вычислить 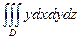, где область D ограничена поверхностями .

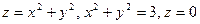Задание 8. Вычислить криволинейный интеграл вдоль линии L от точки A до точки B:

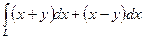, где .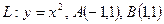

Задание 9. Найти частное решение дифференциального уравнения, удовлетворяющее заданному начальному условию:

.

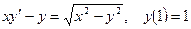Задание 10. Найти общее решение дифференциального уравнения .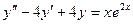

Решение.

Задание 1. Найти неопределенный интеграл .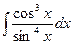

.

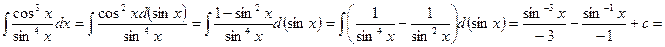
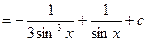Задание 2. Найти площадь фигуры, ограниченной линиями .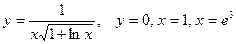

Построим фигуру:

.

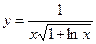
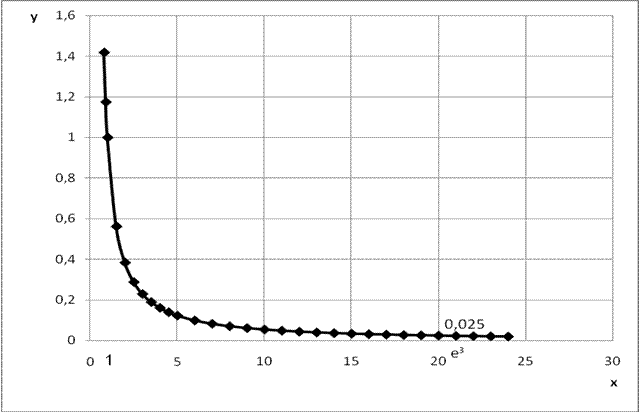
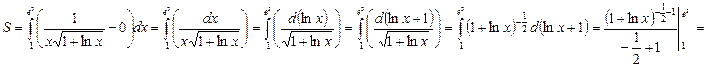
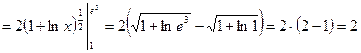Задание 3. Вычислить несобственный интеграл 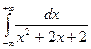или доказать его расходимость.

.

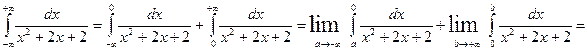
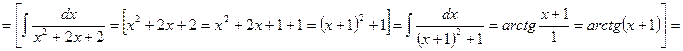
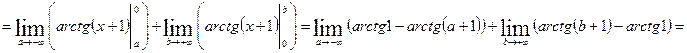
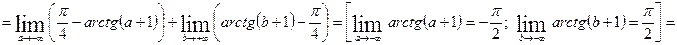
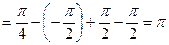Таким образом, интеграл сходится и равен .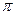

Задание 4. Найти направление, в котором функция 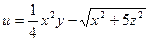возрастает в точке 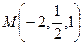быстрее всего.

Направление наискорейшего возрастания функции – это направление вектора градиента, т.е. необходимо найти вектор градиент(grad u) в точке М.

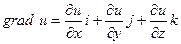
В нашем случае:

,

;

,

;

,

.

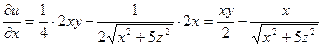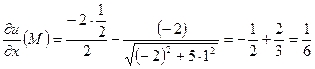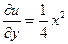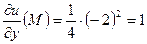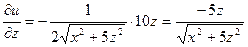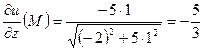Следовательно, .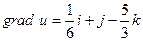

Задание 5. Найти экстремум функции 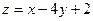при условии, что её аргументы удовлетворяют уравнению .

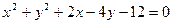Составляем вспомогательную функцию:

.

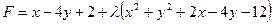Найдем её частные производные и приравниваем их нулю:

, ,

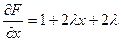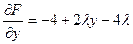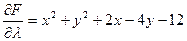
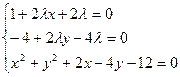
Находим x, y, .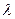

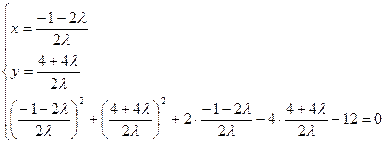
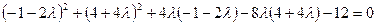
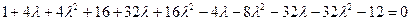
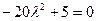
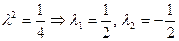
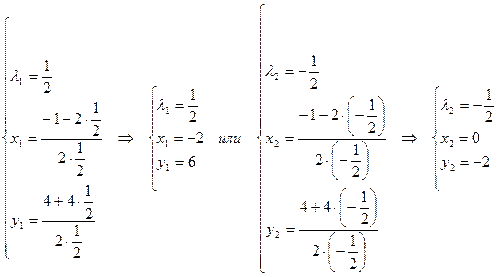
Получим две точк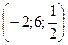и и 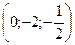для функции F.

Используя достаточные условия проверим где функция F достигает экстремума (если достигает).

Вычислим :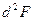

;

;

.

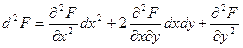
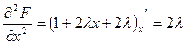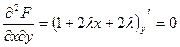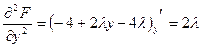Таким образом,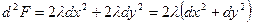

при 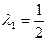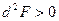, значит в точке 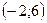функция имеет условный минимум;

при 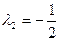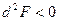, значит в точке 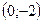функция имеет условный максимум.

;

.

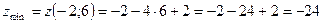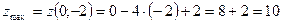Задание 6. Вычислить 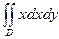, где область D ограничена линиями .

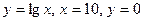Построим область D:

.

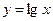
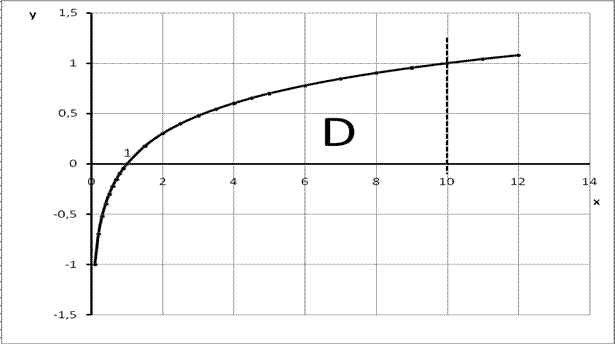
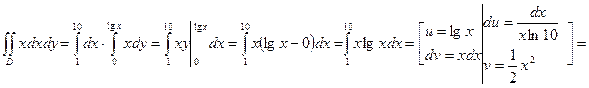
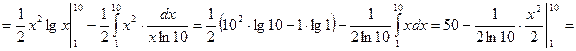
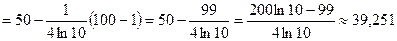Задание 7. Вычислить 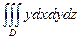, где область D ограничена поверхностями .

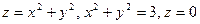Построим область D.

Первое уравнение задает параболоид, второе – круговой цилиндр.

				z
						у
х

.

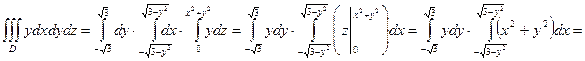
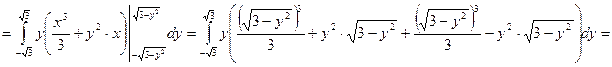
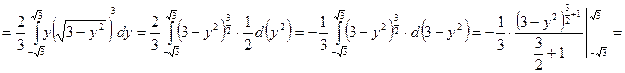
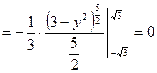Задание 8. Вычислить криволинейный интеграл вдоль линии L от точки A до точки B:

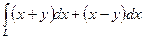, где .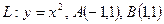

Для вычисления интеграла воспользуемся формулой:

.

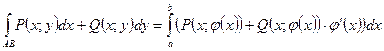Имеем:

.

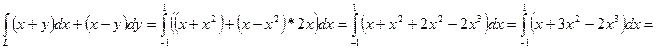
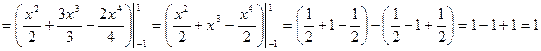Задание 9. Найти частное решение дифференциального уравнения, удовлетворяющее заданному начальному условию:

.

.

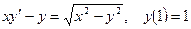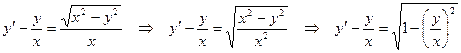Предположим .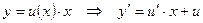

Подставим 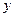и 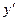в последнее уравнение:

.

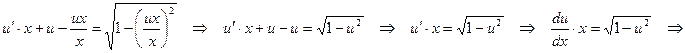
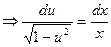Получим уравнение с разделенными переменными.

Интегрируем его:

.

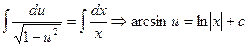Заменим 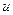на : .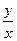

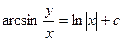Найдем с из условия :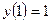

.

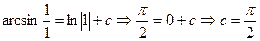Таким образом, частное решение уравнения имеет вид:

.

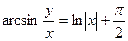Задание 10. Найти общее решение дифференциального уравнения .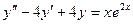

Общее решение имеет вид: 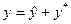, где 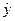- общее решение соответствующего однородного уравнения, 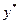- частное решение неоднородного уравнения.

Найдем общее решение уравнения .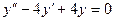

Найдем корни характеристического уравнения .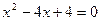

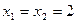(один корень кратности 2).

Значит, общее решение имеет вид: .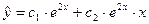

Находим частное решение исходного уравнения. В нем первая часть 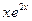есть формула вида 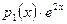, причем 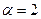является корнем характеристического уравнения, поэтому частное решение 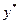будем искать в виде: .

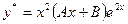Найдем A и B:

,

.

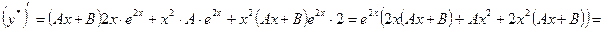
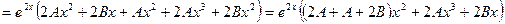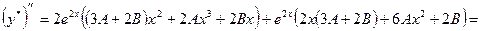
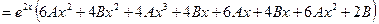Подставляем 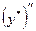, 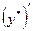и 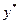в исходное уравнение:

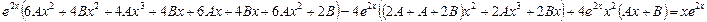Сокращаем на 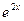и раскрываем скобки:

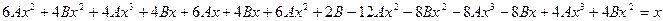
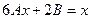
Составляем систему для нахождения A и B:

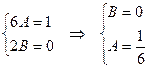
Таким образом .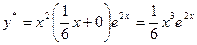

Тогда общее решение исходного уравнения имеет вид:

.

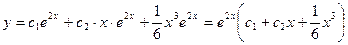Список литературы.

1 Высшая математика: Общий курс: учебник / Под ред. С. А. Самаля. – Минск: Выш. шк., 2000. – 351 с.

2 Гусак, А. А. Высшая математика: учебник / А. А. Гусак. – 4-е изд. – Минск: ТетраСистемс, 2003. – Т. 1. – 544 с.

3 Гусак, А. А. Высшая математика: учебник / А. А. Гусак. – 4-е изд. – Минск: ТетраСистемс, 2004. – Т. 2. – 448 с.

4 Гусак, А. А. Справочник по высшей математике / А. А. Гусак, Г. М. Гусак, Е. А. Бричикова. – 5-е изд. – Минск: ТетраСистемс, 2004. – 640 с.

5 Жевняк, Р. М. Высшая математика: Функции многих переменных. Интегральное исчисление функций одной и многих переменных. Векторный анализ: учебник / Р. М. Жевняк, А. А. Карпук. – Минск: Выш. шк., 1993. – 411с.

6 Сборник задач по математике для втузов. Линейная алгебра и основы математического анализа: учеб. пособие для втузов / В. А. Болтов [и др.]; под ред. А. В. Ефимова и Б. П. Демидовича. – 2-е изд. – М.: Наука, 1986. – Т. 1. –464 с.

7 Сборник задач по математике для втузов. Специальные разделы мате-матического анализа / В. А. Болтов [и др.]; под ред. А. В. Ефимова и Б. П. Де-мидовича. – 2-е изд. – М.: Наука, 1986. – Т. 2. –368 с.

8 Шипачев, В. С. Высшая математика: учебник / В. С. Шипачев. – 7-е изд. – М.: Высш. шк., 2005. – 479 с.