Для независимых событий

Пусть вероятность события B не зависит от по­явления события А.

Событие B называют независимым от события A, если появление события A не изменяет вероятности события B, т. е. если условная вероятность события B равна его безусловной вероятности:

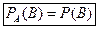(4.4)

Подставив (4.4) в соотношение (4.2), получим

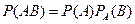= P (В) Р _В(А)= P (А) P (В)

Условная вероятность события A в предположении, что наступило событие B, равна его безусловной вероят­ности. Другими словами, событие A не зависит от со­бытия В.

Итак, если событие B не зависит от события A, то и событие A не зависит от события B; это означает, что свойство независимости событий взаимно.

Для независимых событий теорема умножения P (АВ) = Р (А) Р_А (В) имеет вид

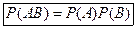, (4.5)

т. е. вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий.

Равенство (3.5) принимают в качестве определения не­зависимых событий.

Два события называют независимыми, если вероятность их совмещения равна произведению вероятностей этих событий; в противном случае события называют зависи­мыми.

На практике о независимости событий заключают по смыслу задачи.

Пример. Найти вероятность совместного поражения цели двумя орудиями, если вероятность поражения цели первым орудием (собы­тие А) равна 0,8, а вторым (событие В) — 0,7.

Решение. Вероятности поражения цели каждым из двух орудий не зависят от того, поразило ли цель другое орудие, поэтому события «первое орудие поразило цель» и «второе орудие поразило цель» неза­висимы.Поэтому, по теореме умножения, искомая вероятность

Р (АВ) = Р(А) Р (В) = 0,7 0,8 = 0,56.

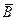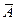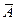Замечание 1. Если события A и B независимы, то незави­симы также события A и , и В, и .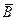

Докажем, что A и 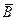независимы.

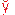Пусть A и B независимые события.

А = A 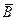+ АВ

События A 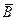и АВ несовместны, тогда

Р(А) = Р(А 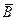)+Р(АВ)= Р(А 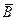) + Р(А)Р(В)

P (A 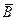)=Р(A)[1 - Р(В)], или Р(А 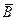)=Р(А)Р( ),

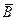т. е. события A и 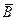независимы.

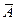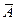Независимость событий и B, и 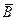- следствие доказанного утверждения.

Несколько событий называют попарно независимыми, если каждые два из них независимы.

Например, события A, В, С попарно независимы, если независимы события A и B, А и C, B и С.

Для того чтобы обобщить теорему умножения на не­сколько событий, введем понятие

независимости событий в совокупности.

Несколько событий называются независимыми в совокуп­ности (или просто независимыми), если независимы ка­ждые два из них и независимы каждое событие и все возможные произведения остальных.

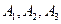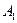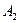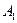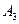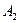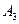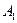Например, если со­бытия независимы в совокупности, то неза­висимы события и , и 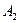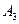, 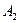и ; и 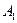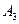, 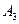и , и 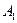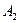. Из сказанного следует, что если события независимы в совокупности, то условная вероят­ность появления любого события из них, вычисленная в предположении, что наступили какие-либо другие собы­тия из числа остальных, равна, его безусловной вероят­ности.

Подчеркнем, что если несколько событий независимы попарно, то отсюда еще не следует их независимость в совокупности. В этом смысле требование независимости событий в совокупности сильнее требования их попарной независимости.

Приведем теперь следствие из теоремы умножения.

Следствие. Вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий:

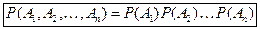. (4.6)

Рассмотрим три события: А, В и С. Совмещение событий А, В и С равносильно сов­мещению событий АВ и C. Так как события А, В и С независимы в совокуп­ности, то независимы, в частности, события АВ и С, а также А и В. По теореме умножения для двух неза­висимых событий имеем:

Р(АВС) = Р (АВ) Р (С) и Р (АВ) =Р(А) Р (В).

Итак, окончательно получим

Р (ABC) = Р (А) Р (В) Р (С).

Для произвольного n доказательство проводится ме­тодом математической индукции.

Замечание. Если события 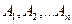независимы в со­вокупности, то и противоположные им события 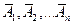также независимы в совокупности.