2015-07-21
376
Известно, что в АИС реакция на любую последовательность получается с помощью свертки этой последовательности и последовательности, называемой импульсной реакцией, или функцией отклика
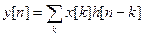(5.6.1)
Предположим, что входная последовательность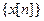 
обладает свойством: 
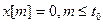. Пусть
, 
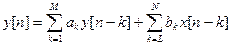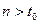
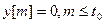, (5.6.2)
где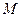 
- натуральное, а 
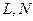- любые целые числа. Эта система будет физически реализуемой, если 
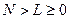. Последовательность, заданная соотношениями (5.6.2) называется рекуррентной, или последовательностью с бесконечным временем отклика.
Пусть имеется АИС с функция отклика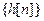 
, на вход которой подается 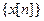, а на выходе получается последовательность 
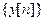. Переходя в (5.6.1) к преобразованиям Фурье, получим
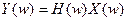(5.6.3).
Функция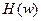 
называется передаточной функцией фильтра. Если выборка велась с частотой 
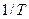, то 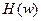будет периодической функцией с периодом 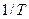. Если последовательность 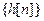- вещественная, то 
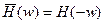. Отсюда следует, функция 
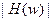является симметричной. В этой связи эту функцию рассматривают лишь на интервале 
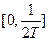и изображают модуль, так как он определяет коэффициент усиления на каждой из частот.
|
|
|
